Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tận dụng kết quả giao tuyến của một mặt phẳng với hai mặt phẳng song song là hai đường thẳng song song, ta có tứ giác A’B’C’D’ là hình bình hành.
Đáp án D.

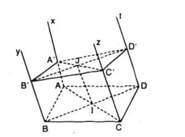
a) Do ABCD là hình bình hành, nên AB // DC
=> AB // (Cz, Dt) (1)
Theo giả thiết Ax // Dt nên Ax // (Cz, Dt) (2)
Từ (1) và (2) suy ra: (Ax, By) // (Cz, Dt)
b) Mặt phẳng β cắt 2 mặt phẳng song song ( Ax, By), (Cz, Dt) theo hai giao tuyến là A’B’và C’D’ nên A’B’// C’D’. (3)
Chứng minh tương tự (Ax, Dt) song song với (By,Cz).Và mặt phẳng β cắt 2 mặt phẳng song song (Ax, Dt), (By, Cz) theo hai giao tuyến là A’D’và B’C’ nên A’D’// B’C’ (4)
Từ (3) và (4) suy ra: tứ giác A’B’C’D’ là hình bình hành.
=> J là trung điểm của A’C’ ( tính chất hình bình hành).
Tứ giác AA’C’C là hình thang vì có: AA’ // CC’ ( giả thiết). Lại có, I và J lần lượt là trung điểm của AC và A’C’ nên IJ là đường trung bình của hình thang
=> IJ// AA’// CC’ ( đpcm).
c) Vì IJ là đường trung bình của hình thang ACC’A’ nên IJ = 1/2(AA’ + CC’)
IJ cũng là đường trung bình của hình thang BDD’B’: IJ = 1/2(BB’ + DD’)
Từ đây suy ra: DD’ + BB’ = AA’ + CC’
=> DD’ = AA’ + CC’ – BB’ = a + c – b

a) Có AA' // DD' và AB//DC nên \(\left(Ax,By\right)\) // \(\left(C_z,D_t\right)\).
b) Do \(\left(Ax,By\right)\) // \(\left(C_z,D_t\right)\) và \(\left(\beta\right)\cap\left(AA'B'B\right)=A'B'\) và \(\left(\beta\right)\cap\left(CC'D'D\right)=C'D'\) nên \(A'B'\) // \(C'D'\).
Chứng minh tương tự B'C'//D'A'.
Do đó tứ giác A'B'C'D' là hình bình hành và J là trung điểm của A'C'.
Suy ra: IJ là đường trung bình của hình thang A'C'CA nên IJ // AA'.
c) Tương tự IJ là đường trung bình của hình thang B'D'DB \(IJ=\dfrac{\left(B'B+DD'\right)}{2}\).
Theo câu b IJ là đường trung bình của hình thang A'C'CA nên \(IJ=\dfrac{\left(AA'+CC'\right)}{2}\).
Suy ra: \(BB'+DD'=AA'+CC'\) hay \(DD'=a+c-b\).

a) Gọi O = AC ∩ BD; O' là trung điểm A'C' thì OO' // AA'
=> OO'// d // b mà O BD
mp (b;d)
=> OO' mp(b;d). Trong mp (b;d) ( mặt phẳng xác định bởi hai đường thẳng song song); d ∩ B'O' = D' là điểm cần tìm
b) Chứng minh mp(a;d) // mp( b;c) , mặt phẳng thứ 3 (A'B'C'D') cắt hai mặt phẳng trên theo hai giao tuyến song song : A'D' // B'C'. Chứng minh tương tự được A'B' // D'C'. Từ đó suy ra A'B'C'D' là hình bình hành

Đáp án C
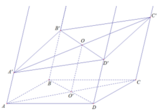
Trên Ax lấy điểm A’ sao cho AA’= x
Trên By lấy điểm B’ sao cho BB’ = y
Trên Cz lấy điểm C’ sao cho CC’ = z
Gọi α là mặt phẳng chứa tia Cz và Dt
Xét (A’B’C’) và α có:
C’ là điểm chung
A’B’ // α
⇒ giao tuyến của α và (A’B’D’) là đường thẳng d đi qua C’ và song song với A’B’
Trong mặt phẳng α , ta có: d cắt Dt tại D’
Gọi O = A C ∩ B D , O ' = A C ' ∩ B ' D '
Xét hình thang AA’C’C có: OO’ là đường trung bình
⇒ O O ' = A A ' + C C ' 2 = x + z 2
Xét tam giác BDD’D có: OO’ là đường trung bình
⇒ O O ' = D D ' + B B ' 2 ⇒ DD’ = x + z – y

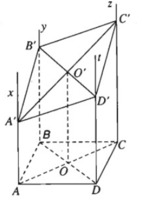
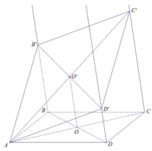
a) Ta có:
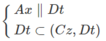
⇒ Ax // (Cz,Dt)
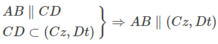
Từ Ax, AB ⊂ (Ax,By) suy ra (Ax, By) // (Cz, Dt)
Tương tự ta có (Ax, Dt) // (By,Cz)
b)
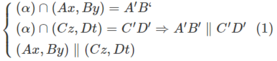
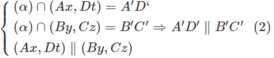
Từ (1) và (2) suy ra tứ giác A’B’C’D’ là hình bình hành.
c) Gọi O, O’ lần lượt là tâm các hình bình hành ABCD, A’B’C’D’. Dễ thấy OO’ là đường trung bình của hình thang AA’, suy ra 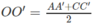
Tương tự ta có:
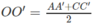

Đáp án D
Trên Bx lấy điểm B’ sao cho BB’ = 4
Trên Dz lấy điểm D’ sao cho DD’ = 2
Gọi α là mặt phẳng chứa tia Bx và Dz
Xét (AB’D’) và α có:
B’ là điểm chung
AD’ // α
⇒ giao tuyến của α và (AB’D’) là đường thẳng d đi qua B’ và song song với AD’
Trong mặt phẳng α , ta có: d cắt Cz tại C’
Gọi O = A C ∩ B D , O ' = A C ' ∩ B ' D '
Xét hình thang BB’D’D có: OO’ là đường trung bình
![]()
Xét tam giác ACC’ có: OO’ là đường trung bình
![]()

Theo định lí 2 ta có: Chỉ có một và một mặt phẳng qua A' // (P). Tương tự với các điểm B', C', D'.
Mà đề bài cho A', B', C', D' đồng phẳng
Suy ra mặt phẳng chứa A', B', C', D' song song với (P)
Do đó: A'D' // AD, B'C' // BC, AD // BC
Suy ra: A'D' // B'C' (1)
Tương tự ta có: A'B' // C'D' (2)
(1)(2) suy ra A'B'C'D' là hình bình hành.
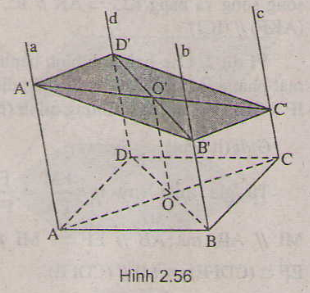
a) Ta có:
\(\left. \begin{array}{l}AA'\parallel DD'\\DD' \subset \left( {CC'D'D} \right)\end{array} \right\} \Rightarrow AA'\parallel \left( {CC'D'D} \right)\)
\(\left. \begin{array}{l}AB\parallel C{\rm{D}}\\C{\rm{D}} \subset \left( {CC'D'D} \right)\end{array} \right\} \Rightarrow AB\parallel \left( {CC'D'D} \right)\)
\(\left. \begin{array}{l}AA'\parallel \left( {CC'D'D} \right)\\AB\parallel \left( {CC'D'D} \right)\\AA',AB \subset \left( {AA'B'B} \right)\end{array} \right\} \Rightarrow \left( {AA'B'B} \right)\parallel \left( {CC'D'D} \right)\)
\(\left. \begin{array}{l}\left( {AA'B'B} \right)\parallel \left( {CC'D'D} \right)\\\left( P \right) \cap \left( {AA'B'B} \right) = A'B'\\\left( P \right) \cap \left( {CC'D'D} \right) = C'D'\end{array} \right\} \Rightarrow A'B'\parallel C'D'\left( 1 \right)\)
\(\left. \begin{array}{l}AD\parallel BC\\BC \subset \left( {BB'C'C} \right)\end{array} \right\} \Rightarrow AD\parallel \left( {BB'C'C} \right)\)
\(\left. \begin{array}{l}AA'\parallel BB'\\BB' \subset \left( {BB'C'C} \right)\end{array} \right\} \Rightarrow AA'\parallel \left( {BB'C'C} \right)\)
\(\left. \begin{array}{l}AA'\parallel \left( {BB'C'C} \right)\\AD\parallel \left( {BB'C'C} \right)\\AA',AD \subset \left( {AA'D'D} \right)\end{array} \right\} \Rightarrow \left( {AA'D'D} \right)\parallel \left( {BB'C'C} \right)\)
\(\left. \begin{array}{l}\left( {AA'D'D} \right)\parallel \left( {BB'C'C} \right)\\\left( P \right) \cap \left( {AA'D'D} \right) = A'D'\\\left( P \right) \cap \left( {BB'C'C} \right) = B'C'\end{array} \right\} \Rightarrow A'D'\parallel B'C'\left( 2 \right)\)
Từ (1) và (2) suy ra \(A'B'C'D'\) là hình bình hành.
Gọi \(O = AC \cap B{\rm{D}},O' = A'C' \cap B'{\rm{D}}'\)
\( \Rightarrow O\) là trung điểm của \(AC,B{\rm{D}}\), \(O'\) là trung điểm của \(A'C',B'{\rm{D}}'\).
\(\left. \begin{array}{l}\left( {AA'B'B} \right)\parallel \left( {CC'D'D} \right)\\\left( {AA'C'C} \right) \cap \left( {AA'B'B} \right) = AA'\\\left( {AA'C'C} \right) \cap \left( {CC'D'D} \right) = CC'\end{array} \right\} \Rightarrow AA'\parallel CC'\)
\( \Rightarrow AA'C'C\) là hình thang
\(O\) là trung điểm của \(AC\)
\(O'\) là trung điểm của \(A'C'\)
\( \Rightarrow OO'\) là đường trung bình của hình thang \(AA'C'C\)
\( \Rightarrow AA' + CC' = 2OO'\left( 3 \right)\)
\(\left. \begin{array}{l}\left( {AA'B'B} \right)\parallel \left( {CC'D'D} \right)\\\left( {BB'D'D} \right) \cap \left( {AA'B'B} \right) = BB'\\\left( {BB'D'D} \right) \cap \left( {CC'D'D} \right) = DD'\end{array} \right\} \Rightarrow BB'\parallel DD'\)
\( \Rightarrow BB'D'D\) là hình thang
\(O\) là trung điểm của \(B{\rm{D}}\)
\(O'\) là trung điểm của \(B'D'\)
\( \Rightarrow OO'\) là đường trung bình của hình thang \(BB'D'D\)
\( \Rightarrow BB' + DD' = 2OO'\left( 4 \right)\)
Từ (3) và (4) suy ra \(AA' + CC' = BB' + DD'\left( { = 2OO'} \right)\).