Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

TenAnh1
TenAnh1
A = (-0.14, -7.4)
A = (-0.14, -7.4)
A = (-0.14, -7.4)
B = (14.46, -7.36)
B = (14.46, -7.36)
B = (14.46, -7.36)
C = (-3.74, -5.6)
C = (-3.74, -5.6)
C = (-3.74, -5.6)
D = (11.62, -5.6)
D = (11.62, -5.6)
D = (11.62, -5.6)
E = (-3.34, -5.86)
E = (-3.34, -5.86)
E = (-3.34, -5.86)
F = (12.02, -5.86)
F = (12.02, -5.86)
F = (12.02, -5.86)
G = (-3.7, -5.88)
G = (-3.7, -5.88)
G = (-3.7, -5.88)
H = (11.66, -5.88)
H = (11.66, -5.88)
H = (11.66, -5.88)
a) Các véctơ cùng phương với là:
,
,
,
,
,
,
.
b) Các véctơ cùng hướng với là:
,
,
.
c) Các véctơ ngược hướng với là:
,
,
,
.

Ta có \(\frac{MA}{MB}=k\Leftrightarrow MA^2=k^2MB^2\Leftrightarrow\overrightarrow{MA^2}=k^2\overrightarrow{MB^2}\)
\(\Leftrightarrow\left(\overrightarrow{MA}-k\overrightarrow{MB}\right)\left(\overrightarrow{MA}+k\overrightarrow{MB}\right)=0\)
Gọi P, Q là các điểm thỏa mãn \(\overrightarrow{PA}.\overrightarrow{MQ}=0\Leftrightarrow MP\perp MQ\)
Từ đó suy ra tập hợp tất cả các điểm M cần tìm là đường tròn đường kính PQ
* Với k=1,quỹ tích cần tìm là đường trung trực (tương ứng mặt phẳng trung trực, với bài toàn trong không gian) của đoạn thẳng AB
* Đường tròn tìm được trong bài trên được gọi là đường tròn Apolonius
* Với bài toàn ở trong không gian, tương tự như vậy, ta cũng thu được quỹ tích là mặt cầu đường kính PQ, và mặt cầu đó cũng được gọi là mặt cầu Apolpnius

Vectơ trong không gian là một đoạn thẳng có định hướng, tức là một đoạn thẳng đã được chỉ rõ điểm đầu và điểm cuối.
Vì các cạnh bên của hình lăng trụ là các đoạn thẳng song song và bằng nhau nên các vectơ bằng vectơ và có điểm đầu và điểm cuối là đỉnh của hình lăng trụ là: các vector BB', CC', DD'.

a) Giả sử A'=(x'; y'). Khi đó \(T_{\overrightarrow{v}}\left(A\right)=A'\Leftrightarrow\left\{{}\begin{matrix}x'=3-1=2\\y'=5+2=7\end{matrix}\right.\)
Do đó: A' = (2;7)
Tương tự B' =(-2;3)
b) Ta có: \(A=T_{\overrightarrow{v}}\left(C\right)\Leftrightarrow C=^T\overrightarrow{-v}\left(A\right)=\left(4;3\right)\)
c) Cách 1. Dùng biểu thức tọa độ của phép tịnh tiến
Gọi M(x;y), M' = \(^T\overrightarrow{v}\) =(x'; y'). Khi đó x' = x-1, y' = y + 2 hay x = x' +1, y= y' - 2. Ta có M ∈ d ⇔ x-2y +3 = 0 ⇔ (x'+1) - 2(y'-2)+3=0 ⇔ x' -2y' +8=0 ⇔ M' ∈ d' có phương trình x-2y+8=0. Vậy \(^T\overrightarrow{v}\) (d) = d'.
Cách 2. Dùng tính chất của phép tịnh tiến
Gọi \(^T\overrightarrow{v}\)(d) =d'. Khi đó d' song song hoặc trùng với d nên phương trình của nó có dạng x-2y+C=0. Lấy một điểm thuộc d chẳng hạn B(-1;1), khi đó \(^T\overrightarrow{v}\) (B) = (-2;3) thuộc d' nên -2 -2.3 +C =0. Từ đó suy ra C = 8.
a) Giả sử A'=(x'; y'). Khi đó
(A) = A' ⇔
Do đó: A' = (2;7)
Tương tự B' =(-2;3)
b) Ta có A = (C) ⇔ C=
(A) = (4;3)
c)Cách 1. Dùng biểu thức tọa độ của phép tịnh tiến
Gọi M(x;y), M' = =(x'; y'). Khi đó x' = x-1, y' = y + 2 hay x = x' +1, y= y' - 2. Ta có M ∈ d ⇔ x-2y +3 = 0 ⇔ (x'+1) - 2(y'-2)+3=0 ⇔ x' -2y' +8=0 ⇔ M' ∈ d' có phương trình x-2y+8=0. Vậy
(d) = d'
Cách 2. Dùng tính chất của phép tịnh tiến
Gọi (d) =d'. Khi đó d' song song hoặc trùng với d nên phương trình của nó có dạng x-2y+C=0. Lấy một điểm thuộc d chẳng hạn B(-1;1), khi đó
(B) = (-2;3) thuộc d' nên -2 -2.3 +C =0. Từ đó suy ra C = 8

Gọi A' và d' theo thứ tự là ảnh của A và d qua phép biến hình trên
a) A' = (-1+2; 2+1) = (1;3), d // d', nên d có phương trình : 3x +y + C = 0. Vì A thuộc d, nên A' thuộc d', do đó 3.1 +3 + C = 0. Suy ra C=-6. Do đó phương trình của d' là 3x+y-6=0
b) A (-1;2) và B(0;-1) thuộc d. Ảnh của A và B qua phép đối xứng qua trục Oy tương ứng là A'(1;2) và B'(0;-1). Vậy d' là đường thẳng A'B' có phương trình :
=
hay 3x - y - 1 =0
c) A'=( 1;-2) , d' có phương trình 3x + y -1 =0
d) Qua phép quay tâm O góc , A biến thành A'( -2; -1), B biến thành B'(1;0). Vậy d' là đường thẳng A'B' có phương trình
=
hay x - 3y + 1 = 0
Gọi A' và d' theo thứ tự là ảnh của A và d qua phép biến hình trên
a) A' = (-1+2; 2+1) = (1;3), d // d', nên d có phương trình : 3x +y + C = 0. Vì A thuộc d, nên A' thuộc d', do đó 3.1 +3 + C = 0. Suy ra C=-6. Do đó phương trình của d' là 3x+y-6=0
b) A (-1;2) và B(0;-1) thuộc d. Ảnh của A và B qua phép đối xứng qua trục Oy tương ứng là A'(1;2) và B'(0;-1). Vậy d' là đường thẳng A'B' có phương trình :
=
hay 3x - y - 1 =0
c) A'=( 1;-2) , d' có phương trình 3x + y -1 =0
d) Qua phép quay tâm O góc , A biến thành A'( -2; -1), B biến thành B'(1;0). Vậy d' là đường thẳng A'B' có phương trình
=
hay x - 3y + 1 = 0

a)
Qua phép đối xứng trục Oy điểm \(M\left(1;1\right)\) biến thành điểm \(M'\left(x;y\right)\) có tọa độ là: \(\left\{{}\begin{matrix}x'=-x=-1\\y'=y=1\end{matrix}\right.\).
Suy ra: \(M'\left(-1;1\right)\).
Qua phép tịnh tiến theo véc tơ \(\overrightarrow{v}\left(2;0\right)\) điểm M' biến thành điểm \(A\left(x_A;y_A\right)\) là:\(\left\{{}\begin{matrix}x_A=-1+2=1\\y_A=0+1=1\end{matrix}\right.\).
Suy ra: \(A\left(1;1\right)\equiv M\) là điểm cần tìm.
b) Gọi C là ảnh của điểm M qua phép tịnh tiến theo véc tơ \(\overrightarrow{v}\)
là: \(\left\{{}\begin{matrix}x_C=2+1=3\\y_C=0+1=1\end{matrix}\right.\). Suy ra: \(C\left(3;1\right)\)
\(M''=Đ_{Oy}\left(C\right)\) nên \(\left\{{}\begin{matrix}x_{M''}=-x_C=-3\\y_{M''}=y_C=1\end{matrix}\right.\). Suy ra: \(M''\left(-3;1\right)\).

Xét tập X = {A, B, C, D, E ; F}. Với mỗi cách chọn hai phần tử của tập X và sắp xếp theo một thứ tự ta được một vectơ thỏa mãn yêu cầu
Mỗi vectơ thỏa mãn yêu cầu tương ứng cho ta một chỉnh hợp chập 2 của 6 phần tử thuộc tập X.
Vậy số các vectơ thỏa mãn yêu cầu bằng số tất cả các chỉnh hợp chập 2 của 6, bằng
Chọn C.
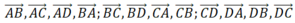
Mỗi cặp sắp thứ tự gồm hai điểm (A; B) cho ta một vectơ có điểm đầu A và điểm cuối B và ngược lại.
Như vậy, mỗi vectơ có thể xem là một chỉnh hợp chập 2 của tập hợp 6 điểm đã cho.
Suy ra có A 6 2 = 30 cách.
Chọn đáp án D.