Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Phương pháp
Giả sử mặt phẳng (b) cắt mặt cầu (S ) theo đường tròn có bán kính r
Mặt cầu (S) có tâm I, bán kính R và d(I; β ) = R ta có R 2 = r 2 + d 2
Cách giải
Mặt phẳng (b) cắt mặt cầu (S) theo đường tròn có bán kính r = 8 π 2 π = 4
Mặt cầu (S) có tâm I(-1;2;3) bán kính R = 17 - m
Ta có
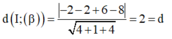
Áp dụng định lí Pytago ta có
![]()
![]()

Chọn C
Mặt cầu (S): x2 + y2 + z2 - 2x + 4y - 4z -16 = 0 có tâm I (1; -2; 2) bán kính R = 5
Khoảng cách từ I (1; -2; 2) đến mặt phẳng (P): x + 2y - 2z - 2 = 0 là 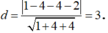
Mặt phẳng cắt mặt cầu theo giao tuyến là một đường tròn có bán kính là: ![]()

Đáp án A.
Phương pháp:
Mặt phẳng (P) cắt (S) theo một đường tròn (C) => Tâm H của (C) là hình chiếu của H trên (P).
Cách giải: Mặt cầu (S) có tâm I(1;2;3) và bán kính R =5
Mặt phẳng (P) cắt (S) theo một đường tròn (C) => Tâm H của (C) là hình chiếu của H trên (P)
![]()
đường thẳng đi qua I và vuông góc với (P) có phương trình
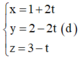
![]()
Thay vào phương trình mặt phẳng (P) ta có:
![]()
![]()

Đáp án C
Phương pháp:
Kiểm tra M nằm trong hay ngoài mặt cầu.
Để giao tuyến là đường tròn có chu vi nhỏ nhất thì bán kính của đường tròn đó là nhỏ nhất
![]()
Cách giải:
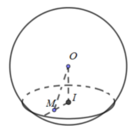
x 2 + y 2 + z 2 = 9 có tâm O(0;0;0)
Nhận xét: Dễ dàng kiểm tra điểm M nằm trong (S), do đó, mọi mặt phẳng đi qua M luôn cắt (S) với giao tuyến là 1 đường tròn.
Để giao tuyến là đường tròn có chu vi nhỏ nhất thì bán kính của đường tròn đó là nhỏ nhất
![]()
![]()
=> IO lớn nhất khi M trùng I hay OM vuông góc với (P)
Vậy, (P) là mặt phẳng qua M và có VTPT là O M → =(1;-1;1)
Phương trình mặt phẳng (P) là:
![]()
![]()

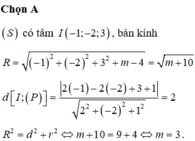




Chọn C
(S) có tâm I (1; -2; 3) và bán kính R = 4
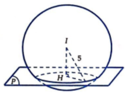
Gọi H là hình chiếu của I lên (P).
(P) cắt mặt cầu (S) theo giao tuyến là đường tròn (T) có chu vi bằng 4π√3
Vậy có 2 giá trị nguyên của m thỏa mãn.