Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Phương pháp:
Công thức khoảng cách từ điểm đến đường thẳng trong không gian:
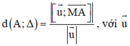 là VTCP của Δ và M là điểm bất kì thuộc
là VTCP của Δ và M là điểm bất kì thuộc
Cách giải:

Độ dài đường cao kẻ từ O của tam giác OAB bằng khoảng cách từ O đến đường thẳng AB:
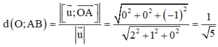

\(\overrightarrow{AA'}=\left(0;0;3\right)=\overrightarrow{BB'}=\overrightarrow{CC'}\)
\(\Rightarrow\left\{{}\begin{matrix}B'\left(0;2;3\right)\\C'\left(-1;0;3\right)\end{matrix}\right.\)
\(\Rightarrow G\left(0;\dfrac{2}{3};3\right)\)

Đáp án D
Cách 1 (Véc tơ đơn vị). Ta có
![]()
=> Tam giác OAB vuông tại O
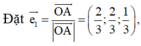
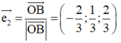

Gọi H, E là các tiếp điểm của đường tròn nội tiếp với các cạnh OA, OB.
Ta có
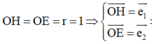
![]()
Cách 2. Kẻ phân giác OE suy ra
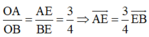
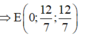
Gọi I là tâm đường tròn nội tiếp tam giác OAB
![]()
Tam giác OAB vuông tại O, có bán kính đường tròn nội tiếp r =1 ⇒ I O = 2
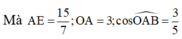
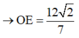
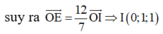
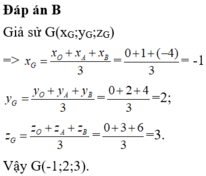
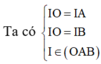
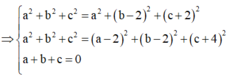
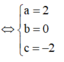
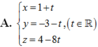
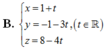
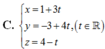
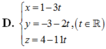
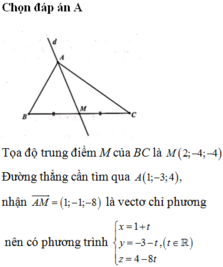
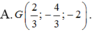
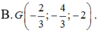
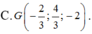
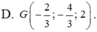

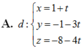
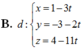
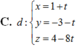
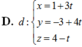
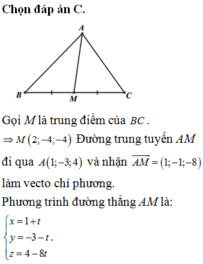

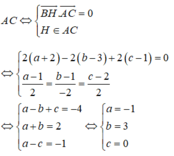

Đáp án A
Ta có: