Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D.
Ta tìm được A ' x 0 ; 0 ; y 0 , C ' 0 ; 1 ; y 0 .
Gọi (P) là mặt phẳng chứa AC' và song song với B'C thì P : y 0 x + x 0 z − x 0 y 0 = 0 .
Do đó
d A C ' , B ' C = d C , P = x 0 y 0 x 0 2 + y 0 2 ≤ 2 2 . x 0 y 0 ≤ 2 4 x 0 + y 0 = 2
Dấu bằng xảy ra khi x 0 = y 0 = 2 .
Tam giác ABC có A B = 4 ; A C = B C = 5 nên có bán kính đường tròn ngoại tiếp là r = 5 2 . Ta lại có B B ' = 2 nên mặt cầu ngoại tiếp hình lăng trụ A B C . A ' B ' C ' có bán kính R = r 2 + 1 4 B B ' 2 = 29 2 .

Đáp án A.
Ta có S : x + a 2 2 + y + b 2 2 + z + c 2 2 = a 2 + b 2 + c 2 4 - d có I - a 2 ; - b 2 ; - c 2
Vì I ∈ d ⇒ I 5 + t ; - 2 - 4 t ; - 1 - 4 t và (S) tiếp xúc với (P) nên d I ; P = R
3 . 5 + t - - 2 - 4 t - 3 . - 1 - 4 t - 1 3 2 + - 1 2 + - 3 2 = 19 ⇔ t + 1 = 1 ⇔ [ t = 0 t = 2
⇒ [ I ( 5 ; - 2 ; - 1 ) I ( 3 ; 6 ; 7 ) ⇒ [ a , b , c , d = - 10 ; 4 ; 2 ; 47 a , b , c , d = - 6 ; - 12 ; - 14 ; 75
Thử lại với a 2 + b 2 + c 2 4 - d = R 2 = 19 thì chỉ có trường hợp {-6;-12;-14;75} thỏa

Đáp án A.
Giả sử mặt cầu (S) có tâm I a ; 0 ; 0 ∈ O x , bán kính R > 0 . Khi đó phương trình mặt cầu (S) là x − a 2 + y 2 + z 2 = R 2 .
Gọi H,K lần lượt là hình chiếu của I trên (P) và (Q) , khi đó:
I H = d I ; P = a + 1 6 và I K = d I ; Q = 2 a − 1 6
Do I H 2 + 4 = R 2 và I K 2 + r 2 = R 2 nên a + 1 2 6 + 4 = R 2 2 a − 1 2 6 + r 2 = R 2
⇒ a + 1 2 6 + 4 = 2 a − 1 2 6 + r 2 ⇔ a + 1 2 + 24 = 2 a − 1 2 + 6 r 2
⇔ a 2 − 2 a + 2 r 2 − 8 = 0 *
Để có duy nhất một mặt cầu (S) thì phương trình (*) phải có một nghiệm
⇔ Δ ' = 1 − 2 r 2 − 8 = 0 ⇔ r 2 = 9 2 . Do r > 0 nên r = 3 2 .







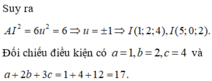

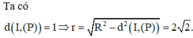
Đáp án D.
Gọi O là trung điểm của AB, suy ra O 0 ; 0 ; 0 .
Ta có A B → = − 2 x 0 ; 0 ; 0 , O C → = 0 ; 1 ; 0 ⇒ A B → . O C → = 0 ⇒ A B ⊥ O C .
Gắn hệ trục tọa độ Oxyz như hình vẽ bên. Với A x 0 ; 0 ; 0 , B − x 0 ; 0 ; 0 , C 0 ; 1 ; 0 , B ' − x 0 ; 0 ; 4 − x 0 , A ' x 0 ; 0 ; 4 − x 0 , C ' 0 ; 1 ; 4 − x 0 do x 0 + y 0 = 4 và 0 < x 0 , y 0 < 4 .
Có A C ' → = − x 0 ; 1 ; 4 − x 0 , B ' C → = x 0 ; 1 ; x 0 − 4 ⇒ A C ' → , B ' C → = 2 x 0 − 8 ; 0 ; − 2 x 0
A C → = − x 0 ; 1 ; 0 ⇒ A C ' → , B ' C → . A C → = − x 0 2 x 0 − 8 = − 2 x 0 x 0 − 4
⇒ d A C ' ; B ' C = A C ' → , B ' C → . A C → A C ' → , B ' C → = 2 x 0 x 0 − 4 4 4 − x 0 2 + 4 x 0 2 = x 0 4 − x 0 4 − x 0 2 + x 0 2
do x 0 ∈ 0 ; 4 .
Với 0 < x 0 < 4 , ta có 4 − x 0 2 + x 0 2 ≥ A M − G M 2 4 − x 0 2 x 0 2 = 2 x 0 4 − x 0 .
Như vậy d A C ' ; B ' C = x 0 4 − x 0 4 − x 0 2 + x 0 2 ≤ x 0 4 − x 0 2 x 0 4 − x 0 = 1 2 .
Dấu “=” xảy ra khi x 0 = 4 − x 0 ⇔ x 0 = 2 = y 0 .
Khi đó A 2 ; 0 ; 0 , B − 2 ; 0 ; 0 , C 0 ; 1 ; 0 , B ' − 2 ; 0 ; 2 . Giả sử phương trình mặt cầu ngoại tiếp lăng trụ A B C . A ' B ' C ' là .
Ta có hệ phương trình sau:
2 2 + 0 2 + 0 2 − 2 a .2 − 2 b .0 − 2 c .0 + d = 0 − 2 2 + 0 2 + 0 2 − 2 a − 2 − 2 b .0 − 2 c .0 + d = 0 0 2 + 1 2 + 0 2 − 2 a .0 − 2 b .1 − 2 c .0 + d = 0 − 2 2 + 0 2 + 2 2 − 2 a − 2 − 2 b .0 − 2 c .2 + d = 0 ⇔ 4 a − d = 4 4 a + d = − 4 2 b − d = 1 4 a − 4 c + d = − 8 ⇔ a = 0 b = − 3 2 c = 1 d = − 4
Vậy mặt cầu (S) có tâm I 0 ; − 3 2 ; 1 và bán kính
R = a 2 + b 2 + c 2 − d = 29 2