Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
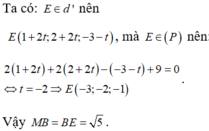
Đáp án A
Đường thẳng d qua A ( 1 ; 2 ; − 3 ) và vuông góc (Q) có phương trình x = 1 + 3 t y = 2 + 4 t z = − 3 − 4 t .
Vì B = d ∩ P ⇒ B 1 + 3 t ; 2 + 4 t ; − 3 − 4 t ∈ P ⇒ t = − 1 ⇒ B − 2 ; − 2 ; 1
Ta có M ∈ P M A ⊥ M B ⇒ M thuộc đường tròn giao tuyến của P và mặt cầu S (tâm I, đường kính AB)
Phương trình mặt cầu S là x + 1 2 2 + y 2 + z + 1 2 = 41 4 .
Và d I , P = 2. − 1 2 + 2.0 + 1 + 9 3 = 3
Khi đó B K = I B 2 − d 2 = 5 2 với K là tâm đường tròn giao tuyến của (P) và (S).
Để MB lớn nhất ⇔ MB là đường kính đường tròn giao tuyến ⇒ M B = 2 B K = 5 .
Đáp án D
Phương trình đường thẳng d : x − 1 3 = y − 2 4 = z + 3 − 3 . Vì B ∈ d ⇒ B 3 b + 1 ; 4 b + 2 ; − 4 b − 3
Mà B = d ∩ P suy ra
Đáp án D
Phương trình đường thẳng
d : x − 1 3 − = y − 2 4 = z + 3 − 4 .
Vì
B ∈ d ⇒ B 3 b + 1 ; 4 b + 2 ; − 4 b − 3
Mà B = d ∩ P suy ra
2 3 b + 1 + 2 4 b + 2 + 4 b + 3 + 9 = 0 ⇔ b = − 1 ⇒ B − 2 ; − 2 ; 1
Gọi A’là hình chiếu của A trên
P ⇒ A A ' : x − 1 2 = y − 2 2 = z + 3 − 1 ⇒ A ' − 3 ; − 2 ; − 1
Theo bài ra, ta có
M A 2 + M B 2 = A B 2 ⇔ M B 2 = A B 2 − M A 2 ≤ A B 2 − A A ' 2 = A ' B 2
Độ dài MB lớn nhất khi
M ≡ A ' ⇒ M B : x = − 2 + t y = − 2 z = 1 + 2 t ⇒ I − 1 ; − 2 ; 3 ∈ M B
Ta thấy 
và 
.
Áp dụng định lý hàm số Cosin cho tam giác MAB ta có:
M A 2 = B A 2 + B M 2 - 2 B A . B M cos 60 o = 6 + 3 2 - 2 6 . 6 2 . 1 2 = 9 2
Suy ra M A = 3 2 2 . Từ đây ta nhận thấy A B 2 = M A 2 + M B 2 nên tam giác MAB vuông tại M và có M A B ^ = 30 o .
Mặt khác:
sin ∆ ^ ; a = 2 + 2 - 1 6 . 6 = 1 2 ⇒ ∆ ^ ; a = 30 o = M A B ^ .
Từ đó suy ra M chính là hình chiếu của B lên mặt phẳng (a).
Khi đó M B : x - 2 2 = y - 2 1 = z - 6 - 1
nên M ( 2m + 2; m + 2; -m + 6 )
Vì M thuộc mặt phẳng (a) nên
2( 2m + 2 ) + ( m + 2 ) - ( -m + 6 ) + 3 = 0 ⇒ m = - 1 2
Vậy M 1 ; 3 2 ; 13 2
Đáp án A
Chọn đáp án C
Mặt cầu (S) có tâm I(4;3;3) và bán kính R = 4. Gọi I’ là hình chiếu của I trên mặt phẳng α .
Đường thẳng I I ' đi qua I(4;3;3) và nhận n = ⇀ 1 ; 1 ; 1 làm vectơ chỉ phương nên có phương trình là:
Tọa độ điểm I’ thỏa mãn hệ
⇔ t = - 2 . Suy ra I’(2;1;1).
Gọi hình tròn (C) bán kính r là thiết diện của khối cầu (S) khi cắt bởi mặt phẳng α . Khi đó I’ là tâm của đường tròn (C).
Ta có I M = 14 < 4 = R và M ∈ α nên điểm M thuộc miền trong của đường tròn (C) (M nằm trong hình trong hình tròn).
Do đường thẳng d ⊂ α , d đi qua M và d cắt mặt cầu tại hai điểm A, B nên d cắt đường tròn (C) tại hai điểm A, B.
Phương tích của điểm M với đường tròn (C): M A . M B = r 2 - I ' M 2 .
Do r không đổi nên r 2 - I ' M 2 không đổi ⇒ M A . M B không đổi.
Lại có
Dấu “=” xảy ra khi MA = MB hay A B ⊥ M I ' .
Mà A B ⊥ M I ' nên đường thẳng AB có một vectơ chỉ phương là u ⇀ = I I ' ; ⇀ M I ' ⇀ = 2 ; - 4 ; 2 (cùng phương với vectơ u 2 ⇀ )
