Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Veto chỉ phương ![]()
Đi qua ![]()
Phương trình đường thẳng cần tìm có dạng:
![]()

\(\overrightarrow{AB}=\left(1;2;3\right)\) ; \(\overrightarrow{CD}=\left(1;1;1\right)\)
\(\left[\overrightarrow{AB};\overrightarrow{CD}\right]=\left(-1;2;-1\right)=-\left(1;-2;1\right)\)
Phương trình (P):
\(1\left(x-1\right)-2y+1\left(z-1\right)=0\Leftrightarrow x-2y+z-2=0\)
Để tìm phương trình mặt phẳng (P) ta cần tìm được vector pháp tuyến của mặt phẳng. Vì mặt phẳng (P) song song với đường thẳng AB nên vector pháp tuyến của (P) cũng vuông góc với vector chỉ phương của AB, tức là AB(1-0;2-0;4-1)=(1;2;3).
Vì (P) đi qua C(1;0;1) nên ta dễ dàng tìm được phương trình của (P) bằng cách sử dụng công thức phương trình mặt phẳng:
3x - 2y - z + d = 0, trong đó d là vế tự do.
Để tìm d, ta chỉ cần thay vào phương trình trên cặp tọa độ (x;y;z) của điểm C(1;0;1):
3(1) -2(0) - (1) + d = 0
⇒ d = -2
Vậy phương trình của mặt phẳng (P) là:
3x - 2y - z - 2 = 0,
và đáp án là B.

a. Mặt phẳng (P) có (3;-2;2) là 1 vtpt nên d nhận (3;-2;2) là 1 vtcp
Phương trình tham số d: \(\left\{{}\begin{matrix}x=1+3t\\y=2-2t\\z=-1+2t\end{matrix}\right.\)
b. \(\overrightarrow{n_{\left(P\right)}}=\left(1;1;1\right)\) ; \(\overrightarrow{n_{\left(P'\right)}}=\left(1;-1;1\right)\)
\(\left[\overrightarrow{n_{\left(P\right)}};\overrightarrow{n_{\left(P'\right)}}\right]=\left(2;0;-2\right)=2\left(1;0;-1\right)\)
\(\Rightarrow\) d nhận (1;0;-1) là 1 vtcp nên pt có dạng: \(\left\{{}\begin{matrix}x=1+t\\y=-2\\z=3-t\end{matrix}\right.\)
c. \(\overrightarrow{u_{\Delta}}=\left(3;2;1\right)\) ; \(\overrightarrow{u_{\Delta'}}=\left(1;3;-2\right)\)
\(\left[\overrightarrow{u_{\Delta}};\overrightarrow{u_{\Delta'}}\right]=\left(-7;7;7\right)=7\left(-1;1;1\right)\)
Đường thẳng d nhận (-1;1;1) là 1 vtcp nên pt có dạng: \(\left\{{}\begin{matrix}x=-1-t\\y=1+t\\z=3+t\end{matrix}\right.\)

Ta có: \(\overrightarrow{BC}=\left(-1;-6;3\right)\)
Đường thẳng song song với \(BC\) nên nó nhận \(\overrightarrow{BC}\) làm VTCP
\(\Rightarrow\) Phương trình tham số của đường thẳng đi qua \(A\) và song song với \(BC\) là: \(\left\{{}\begin{matrix}x=1-t\\y=-1-6t\\z=3+3t\end{matrix}\right.\quad\left(t\in R\right)\).

Đáp án C
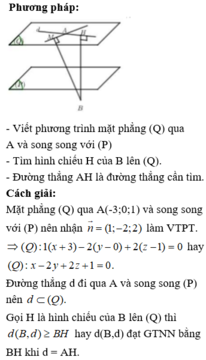
Phương pháp
Gọi H là hình chiếu của B trên mặt phẳng (Q) đi qua A và song song với (P). Khi đó
![]()
![]()
Cách giải
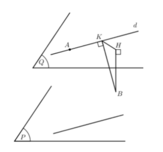
![]()
Gọi (Q) là mặt phẳng đi qua A và song song với (P) ta tìm được phương trình mặt phẳng (Q): (P): x-2y+2z-5=0, khi đó d ∈ (Q)
Gọi H là hình chiếu của B trên (Q) ta có
![]()
![]()
Phương trình đường thẳng d’ đi qua B và vuông góc với (Q) là
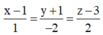
![]()
![]()
![]()
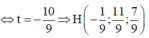
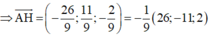
Vậy phương trình đường thẳng d cần tìm là d:
x + 3 26 = y 11 = z - 1 2

Gọi (Q) là mặt phẳng đi qua A và song song với (P) thì phương trình của (Q) là (x + 2) + 2(y + 1) - (z - 1) = 0 hay x + 2y - z + 5 = 0. Gọi H là hình chiếu vuông góc của B lên (Q). Giả sử Δ là đường thẳng qua A và song song với (P), I là chân đường vuông góc kẻ từ B đến ∆ . Khi đó I ∈ (Q) và BH ≤ BI.
Do đó AH chính là đường phải tìm.
Gọi d là đường thẳng đi qua B và vuông góc với (Q).
Phương trình của d là:
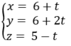
Để tìm giao điểm H = d ∩ (Q) ta thay phương trình của d vào phương trình của (Q), ta có:
6 + t + 2(6 + 2t) - (5 - t) + 5 = 0 ⇒ t = -3.
Do đó H = (3; 0; 8)
Phương trình đường thẳng AH là:
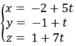

Đáp án A
Trục Ox có vecto chỉ phương là u → =(1;0;0) và A B → =(-2;2;1)
Mà (P) chứa A, B và (P)//Ox
⇒ n ( P ) → = u → . A B → = ( 0 ; - 1 ; 2 )
Vậy phương trình mặt phẳng (P) là:
y-2z+2=0
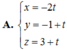


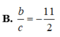
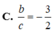
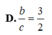
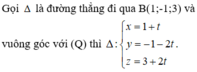
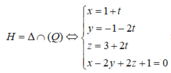
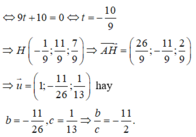
a. \(\overrightarrow{MN}=\left(2;2-2\right)=2\left(1;1;-1\right)\)
Phương trình tham số MN: \(\left\{{}\begin{matrix}x=1+t\\y=t\\z=1-t\end{matrix}\right.\)
b. \(\overrightarrow{BC}=\left(2;1;1\right)\Rightarrow d\) nhận (2;1;1) là 1 vtpt
Phương trình d: \(\left\{{}\begin{matrix}x=2t\\y=-1+t\\z=3+t\end{matrix}\right.\)