Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi mặt phẳng là (P) dễ kí hiệu
\(d\left(M;\left(P\right)\right)=\frac{\left|-6+2+2-7\right|}{\sqrt{2^2+2^2+1}}=\frac{9}{3}=3\)
Áp dụng định lý Pitago:
\(R=\sqrt{3^2+4^2}=5\)
Phương trình mặt cầu:
\(\left(x+3\right)^2+\left(y-1\right)^2+\left(z-2\right)^2=25\)
\(\Leftrightarrow x^2+y^2+z^2+6x-2y-4z-11=0\)

3.
\(d\left(I;\left(P\right)\right)=\frac{\left|-1-4-2-2\right|}{\sqrt{1^2+2^2+2^2}}=3\)
Áp dụng định lý Pitago:
\(R=\sqrt{5^2+3^2}=\sqrt{34}\)
Pt mặt cầu:
\(\left(x+1\right)^2+\left(y-2\right)^2+\left(z+1\right)^2=34\)
\(\Leftrightarrow x^2+y^2+z^2+2x-4y+2z-28=0\)
4.
\(\left(\alpha\right)\) nhận \(\left(2;-3;-4\right)\) là 1 vtpt và tất cả các vecto có dạng \(\left(2k;-3k;-4k\right)\) cũng là các vecto pháp tuyến với \(k\ne0\) (bạn tự tìm đáp án phù hợp)
5.
\(\overrightarrow{AB}=\left(3;-6;0\right)\) ; \(\overrightarrow{AC}=\left(5;3;3\right)\)
\(\Rightarrow\left[\overrightarrow{AB};\overrightarrow{AC}\right]=\left(-18;-9;39\right)=-3\left(6;3;-13\right)\)
Mặt phẳng (ABC) nhận \(\left(6;3;-13\right)\) là 1 vtpt
Phương trình:
\(6\left(x+1\right)+3\left(y-2\right)-13\left(z-3\right)=0\)
\(\Leftrightarrow6x+3y-13z+39=0\)
1.
\(\overrightarrow{IA}=\left(4;2;6\right)\Rightarrow R^2=IA^2=4^2+2^2+6^2=56\)
Pt mặt cầu:
\(\left(x-1\right)^2+\left(y+3\right)^2+\left(z+2\right)^2=56\)
Dạng khai triển:
\(x^2+y^2+z^2-2x+6y+4z-42=0\)
2.
\(\overrightarrow{BA}=\left(10;2;-12\right)\Rightarrow R=\frac{AB}{2}=\frac{1}{2}\sqrt{10^2+2^2+12^2}=\sqrt{62}\)
Gọi I là trung điểm AB \(\Rightarrow I\left(1;1;1\right)\)
Pt mặt cầu:
\(\left(x-1\right)^2+\left(y-1\right)^2+\left(z-1\right)^2=62\)
\(\Leftrightarrow x^2+y^2+z^2-2x-2y-2z-59=0\)

Bán kính mặt cầu: \(R=\sqrt{1^2+\left(-2\right)^2+1^2+8}=\sqrt{14}\)
Tâm mặt cầu: \(I\left(1;-2;1\right)\)
\(\Rightarrow d\left(I;\left(Q\right)\right)=\sqrt{R^2-\left(\frac{R}{2}\right)^2}=\frac{\sqrt{42}}{2}\)
Do (Q) song song (P) nên pt (Q) có dạng: \(2x+3y+z+d=0\)
Áp dụng công thức khoảng cách:
\(d\left(I;\left(Q\right)\right)=\frac{\left|2-6+1+d\right|}{\sqrt{2^2+3^2+1}}=\frac{\sqrt{42}}{2}\)
\(\Leftrightarrow\left|d-3\right|=7\sqrt{3}\Rightarrow\left[{}\begin{matrix}d=3+7\sqrt{3}\\d=3-7\sqrt{3}\end{matrix}\right.\)
Có 2 mặt phẳng thỏa mãn: \(\left[{}\begin{matrix}2x+3y+z+3+7\sqrt{3}=0\\2x+3y+z+3-7\sqrt{3}=0\end{matrix}\right.\)

Lời giải:
b/ $x^2-4x+20=0$
$\Leftrightarrow (x-2)^2+16=0\Leftrightarrow (x-2)^2=-16< 0$ (vô lý)
Do đó pt vô nghiệm.
c/ $2x^3-3x+1=0$
$\Leftrightarrow 2x^2(x-1)+2x(x-1)-(x-1)=0$
$\Leftrightarrow (x-1)(2x^2+2x-1)=0$
$\Rightarrow x-1=0$ hoặc $2x^2+2x-1=0$
$\Leftrightarrow x=1$ hoặc $x=\frac{-1\pm \sqrt{3}}{2}$



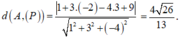

Đáp án C
Điểm M(x,y,z) cách đều hai mặt phẳng (P) và (Q) khi và chỉ khi