Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn A
Gọi I (a;b;c)
Ta có IA=IO=R ó hình chiếu của I lên OA là trung điểm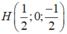 
của OA.
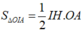
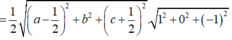
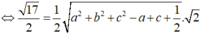
Theo bài ra ta có:
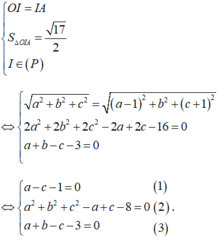
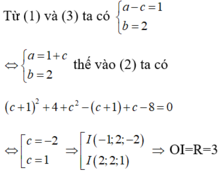
Đáp án A
Mặt cầu (S): (x-a)²+(y-b)²+(z-c)²=R² có tâm là I(a;b;c) và bán kính là R.
Do đó, mặt cầu (S): (x-1)²+(y+2)²+z²=25 có tâm I(1;-2;0) và bán kính R=5.
4.
Bán kính mặt cầu bằng khoảng cách từ A đến Ox
Trục Ox nhận \(\overrightarrow{u}=\left(1;0;0\right)\) là vtcp
Khoảng cách từ A đến Ox:
\(d\left(A;Ox\right)=\frac{\left|\left[\overrightarrow{OM};\overrightarrow{u}\right]\right|}{\left|\overrightarrow{u}\right|}=\frac{\left|\left(0;4;-3\right)\right|}{\left|\left(1;0;0\right)\right|}=\frac{\sqrt{4^2+3^2}}{1}=5\)
\(\Rightarrow R=5\)
5.
\(\overrightarrow{AB}=\left(0;2;0\right)\) ; \(\overrightarrow{BC}=\left(2;0;-2\right)\) ; \(\overrightarrow{BD}=\left(0;0;-3\right)\)
Gọi M là trung điểm AB \(\Rightarrow M\left(1;1;1\right)\)
Phương trình mặt phẳng trung trực của AB: \(y-1=0\)
Gọi N là trung điểm BC \(\Rightarrow N\left(2;2;0\right)\)
Phương trình mặt phẳng trung trực của BC:
\(1\left(x-2\right)-1\left(z-0\right)=0\Leftrightarrow x-z-2=0\)
Gọi P là trung điểm BD \(\Rightarrow P\left(1;2;-\frac{1}{2}\right)\)
Phương trình mặt phẳng trung trực BD:
\(z+\frac{1}{2}=0\)
Tọa độ tâm I của mặt cầu là nghiệm: \(\left\{{}\begin{matrix}y-1=0\\x-z-2=0\\z+\frac{1}{2}=0\end{matrix}\right.\) \(\Rightarrow I\left(\frac{5}{2};1;-\frac{1}{2}\right)\)
\(\Rightarrow\overrightarrow{AI}=\left(\frac{3}{2};1;-\frac{3}{2}\right)\Rightarrow R=IA=\frac{\sqrt{22}}{2}\)
Bạn kiểm tra lại quá trình tính toán nhé
6.
\(\overrightarrow{AB}=\left(2;2;4\right)=2\left(1;1;2\right)\)
Gọi M là trung điểm AB \(\Rightarrow M\left(2;1;-1\right)\)
Phương trình mp trung trực AB:
\(1\left(x-2\right)+1\left(y-1\right)+2\left(z+1\right)=0\)
\(\Leftrightarrow x+y+2z-1=0\)
Chọn C
Gọi tọa độ điểm M(x;y;z)
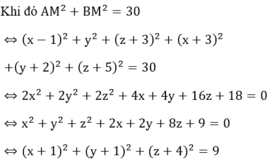
là phương trình của mặt cầu (S), có tâm I (-1;-1;-4) và bán kính R = 3
Đáp án C
là trung điểm của AB khi đó M A 2 + M B 2 = 30
Suy ra
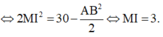
Do đó mặt cầu (S) tâm I(-1;-1;-4), R =3
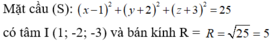
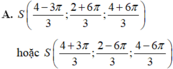
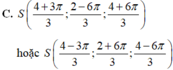
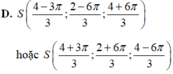
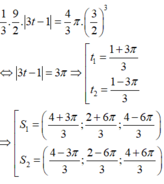
Đáp án C
Do ABCD là tứ diện đều nên H là trọng tâm tam giác BCD và I trùng với trọng tâm G của tứ diện ABCD. Ta có:
Từ đó ta có:
Vậy đáp án C đúng.