Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D.
Mặt cầu (S) có tâm I 1 ; − 2 ; 3 và bán kính R=5 . Mặt phẳng Q / / P nên (Q) có phương trình là 2 x + 2 y − z + m = 0, m ≠ 17 .
Mặt phẳng (Q) cắt mặt cầu (S) theo giao tuyến là đường tròn có bán kính r, chu vi bằng 6 π nên 2 π r = 6 π ⇔ r = 3 .
Khoảng cách từ I đến mặt phẳng (Q) là d I ; Q = R 2 − r 2 = 5 2 − 3 2 = 4 .
Khi đó
2.1 + 2. − 2 − 3 + m 2 2 + 2 2 + − 1 2 = 4 ⇔ m − 5 = 12 ⇔ m − 5 = 12 m − 5 = − 12 ⇔ m = 17 L m = − 7 t m
Vậy phương trình mặt phẳng (Q) là 2 x + 2 y − z − 7 = 0

Do β / / α nên β : 2 x + 2 y - z + D = 0 D ≠ 17
Mặt cầu (S) có tâm I ( 1;-2;3 ), bán kính R = 5
Đường tròn có chu vi là 6 π nên bán kính của đường tròn này là r = 3
Ta có
d I β = R 2 - r 2 ⇔ 2 . 1 + 2 . - 2 - 3 + D 2 2 + 2 2 + - 1 2 = 4 ⇔ D - 5 = 12 ⇔ D = - 7 D = 17
Đáp án B

Đáp án B
Mặt cầu (S) có tâm I(1;-1;2) và bán kính ![]()
Ta có (Q) // (P) nên (Q) có dạng: ![]()
Mặt phẳng (Q) cắt (S) theo 1 đường tròn có bán kính
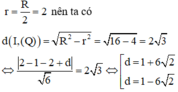
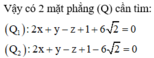


HD: Dễ thấy (P)//(Q). Gọi (R) là mặt phẳng song song và cách đều 2 mặt phằng (P) và (Q)



 bit lm bài này k giup tui
bit lm bài này k giup tui


Đáp án D