
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


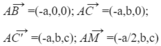

Chọn C
Ta chia khối hộp chữ nhật ABCD.A’B’C’D’ thành các hình chóp có thể tích:
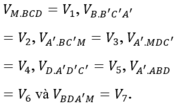
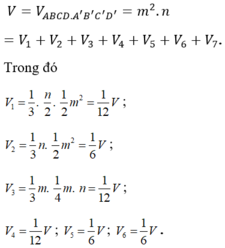
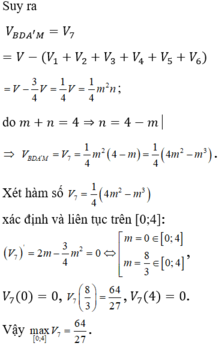

O A B C D B' A' D' C' M K O a a
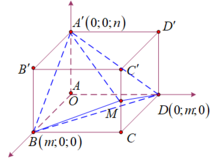
a. Từ giả thiết ta có :
\(C\left(a;a;0\right);C'\left(a;a;b\right);D'\left(0;a;b\right);B'\left(a;0;b\right)\)
Vì M là trung điểm của CC' nên \(M=\left(a;a;\frac{b}{2}\right)\)
Ta có :
\(\overrightarrow{BD}=\left(-a;a;0\right)\)
\(\overrightarrow{BA}=\left(-a;0;b\right)\)
\(\overrightarrow{BM}=\left(0;a;\frac{b}{2}\right)\)
Vì thế \(\left[\overrightarrow{BD};\overrightarrow{BA'}\right]=\left(\left|\begin{matrix}a&0\\0&b\end{matrix}\right|;\left|\begin{matrix}0&-a\\b&-a\end{matrix}\right|;\left|\begin{matrix}-a&a\\-a&0\end{matrix}\right|\right)\)
\(=\left(ab,ab,a^2\right)\)
Vậy \(V_{BDa'M}=\frac{1}{6}\left|\left[\overrightarrow{BD};\overrightarrow{BA'}\right].\overrightarrow{BM}\right|=\frac{1}{6}\left|a^2b+\frac{a^2b}{2}\right|=\frac{a^2b}{4}\)
b. Gọi K là trung điểm của BD. Do \(A'B=A'D\Rightarrow A'K\perp BD\)
Lại có \(MB=MD\Rightarrow MK\perp BD\)
Vậy \(\widehat{A'KM}=90^0\)
\(\Leftrightarrow\overrightarrow{A'K}.\overrightarrow{MK}=0\)
Ta có :
\(K=\left(\frac{a}{2};\frac{a}{2};0\right)\) do đó :
\(\overrightarrow{A'K}=\left(\frac{a}{2};\frac{a}{2};-b\right)\)
\(\overrightarrow{MK}=\left(-\frac{a}{2};\frac{-a}{2};\frac{-b}{2}\right)\)
Vậy \(\left(1\right)\Leftrightarrow-\frac{a^2}{4}-\frac{a^2}{4}+\frac{b^2}{2}=0\)
\(\Leftrightarrow b^2=a^2\)
\(\Leftrightarrow\frac{a}{b}=1\)
Do (a>0,b>0) vì thế \(\left(A'BD\right)\perp\left(MBD\right)\Leftrightarrow\frac{a}{b}=1\)

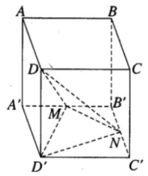
Thể tích khối chóp D’.DMN bằng thể tích khối chóp D.D’MN
Ta có: S D ' MN = S A ' B ' C ' D ' - S D ' A ' M + S D ' C ' N + S B ' MN
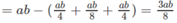
Thể tích khối chóp
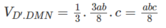
Từ đó suy ra tỷ số giữa thể tích khối chóp D’.DMN và thể tích khối hộp chữ nhật ABCD.A’B’C’D’ bằng 1/8

Đáp án C
Phương pháp
+) Gọi A(a;0;0), B(0;b;0), C(0;0;c) (a, b, c ≠ 0) viết phương trình mặt phẳng (P) đi qua A, B, C dạng đoạn chắn.M ∈ (P)=> Thay tọa độ điểm M vào phương trình mặt phẳng (P).
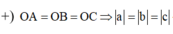
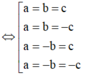
+) Ứng với mỗi trường hợp tìm các ẩn a, b, c tương ứng
Cách giải
Gọi A(a;0;0), B(0;b;0), C(0;0;c) (a, b, c ≠ 0) khi đó phương trình mặt phẳng đi qua A, B, C là
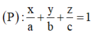
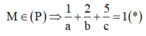
![]()
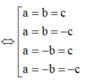
TH1: a=b=c thay vào (*) có
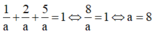
![]()
TH2: a=b=-c thay vào (*) có
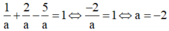
![]()
TH3: a=-b=c thay vào (*) có
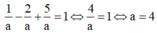
![]()
TH4: a=-b=-c thay vào (*) có
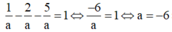
![]()
Vậy có 4 mặt phẳng thỏa mãn.

câu 5 ấy chắc thầy tui buồn ngủ nên quánh lộn chữ sai thành đúng r
12.
\(R=d\left(I;Oxz\right)=\left|y_I\right|=3\)
Phương trình:
\(x^2+\left(y+3\right)^2+z^2=9\)
\(\Leftrightarrow x^2+y^2+z^2+6y=0\)
13.
\(R=d\left(M;\alpha\right)=\frac{\left|1-1+2.2-3\right|}{\sqrt{1^2+1^2+2^2}}=\frac{1}{\sqrt{6}}\)
Pt mặt cầu:
\(\left(x-1\right)^2+\left(y-1\right)^2+\left(z+2\right)^2=\frac{1}{6}\)
14.
\(R=d\left(I;\left(P\right)\right)=\frac{\left|-1-4-2-2\right|}{\sqrt{1^2+2^2+2^2}}=3\)
Phương trình:
\(\left(x+1\right)^2+\left(y-2\right)^2+\left(z-1\right)^2=9\)
\(\Leftrightarrow x^2+y^2+z^2+2x-4y-2z-3=0\)