Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án C.

nên một vectơ chỉ phương của đường phân giác của góc nhọn tạo bởi d và Δ là
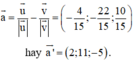
Nhận thấy tọa độ điểm A thỏa mãn phương trình ở phương án C nên phương án đúng là C.
Cách 2: Đường thẳng d và đường thẳng Δ có vectơ chỉ phương lần lượt là
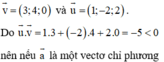
của đường phân giác của góc nhọn tạo bởi d và Δ thì
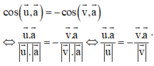
Kiểm tra từng phương án đến khi tìm được phương án đúng.
Tọa độ của điểm A không thỏa mãn phương trình ở phương án B nên loại phương án này.
- Phương án A: Đường thẳng có vectơ chỉ phương ![]()


Đáp án D
Phương pháp: △ ⊥ d △ ⊥ A B ⇒ u △ → = u d → ; A B →
Viết phương trình đường thẳng biết điểm đi qua và VTCP.
Cách giải: d; x + 1 - 2 = y - 2 1 = z - 3 3 có 1 VTCP u → - 2 ; 1 ; 3 ; A B → = - 2 ; 3 ; 2
∆ vuông góc với d và AB => AB nhận u → - 2 ; 1 ; 3 và A B → = - 2 ; 3 ; 2 là cặp VTPT
=> ∆ có 1 VTCP v → = A B → ; u → = ( 7 ; 2 ; 4 )
Phương trình đường thẳng ∆: x - 1 7 = y + 1 2 = z - 1 4

Đường thẳng d đi qua A ( 1;-1;2 ) có vec tơ chỉ phương u → ( a ; b ; c ) do d song song (P): 2x - y - z + 3 = 0 nên u → ( a ; b ; c ) ⊥ n ( 2;-1;1 )
⇔ u → . n = 0 ⇔ 2a = b + c
Đến đây ta kiểm tra chỉ có đáp án A là đường thẳng có véc tơ chỉ phương thỏa mãn (1) nên ta chọn đáp án A
Đáp án cần chọn là A

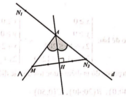




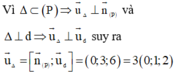
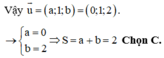


Chọn đáp án B