Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét phương trình \(\left| {17cos5\pi t} \right| = 10\)
\(\begin{array}{l} \Leftrightarrow \left[ \begin{array}{l}17cos5\pi t = 10\\17cos5\pi t =-10\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}cos5\pi t = \frac{{10}}{{17}}\\cos5\pi t = -\frac{{10}}{{17}}\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}5\pi t = \pm 0,9 + k2\pi \\5\pi t = \pm 2,2 + k2\pi \end{array} \right.\left( {k\; \in \;\mathbb{Z}} \right)\\ \Leftrightarrow \left[ \begin{array}{l}t = \pm 0,06 + k\frac{2}{5}\\t = \pm 0,14 + k\frac{2}{5}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\)
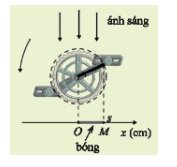
Độ dài bóng \(|x|\;\)bằng 10 cm tại các thời điểm \(t = \pm 0,06 + k\frac{2}{5}\),\(t = \pm 0,14 + k\frac{2}{5}\),\(k \in \mathbb{Z}\).

Độ dài bóng OM bằng 10 cm khi s = 10 hoặc s = -10.
Khi s = 10. Ta có: \(17cos5\pi t = 10 \Leftrightarrow cos5\pi t = \frac{{10}}{{17}}\)
Khi s = 10. Ta có: \(17cos5\pi t = - 10 \Leftrightarrow cos5\pi t = \frac{{ - 10}}{{17}}\)
Từ đó, ta có thể xác định được các thời điểm t bằng cách giải phương trình côsin.

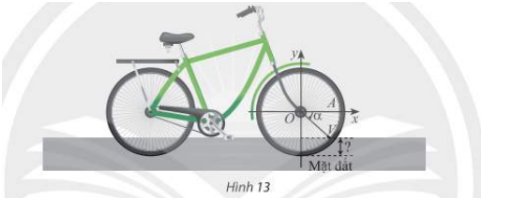
Sau một phút di chuyển, van V đã quay được một góc lượng giác có số đo góc là: \(\alpha=11\cdot60=660\left(rad\right)\)
Khi đó tọa độ điểm V biểu diễn cho góc lượng giác trên có tọa độ là: \(V\left(58\cdot cos\alpha,58\cdot sin\alpha\right)\approx\left(56;15,2\right)\)
Từ đó, khoảng cách từ van đến mặt đất khoảng \(58-15,2\approx42,8\left(cm\right)\)

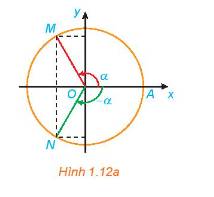
a) Hai điểm M và N đối xứng nhau qua hệ trục Oxy.
Suy ra
\(\cos ( - \alpha )\)=\(\cos \alpha \); \(\sin ( - \alpha )\)= \( - \sin \alpha \)
b) Ta có:
\(\tan ( - \alpha )\) =\( - \tan \alpha \); \(\cot ( - \alpha )\)\( - \cot \alpha \)

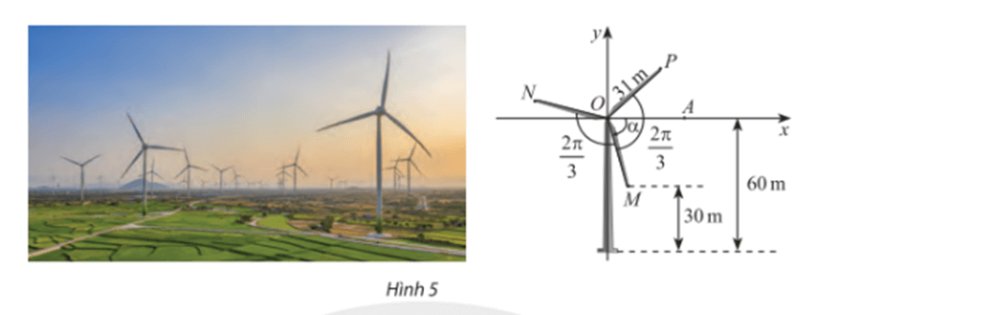
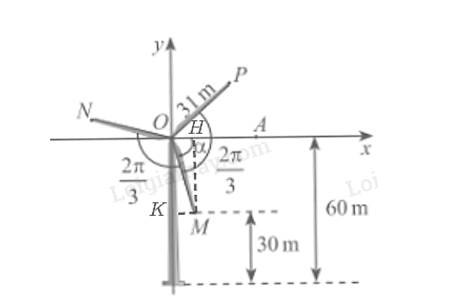
a, Từ điểm M kẻ MH vuông góc với Ox, MK vuông góc với Oy.
Ta có: MH = 60 – 30 = 30 m.
Khi đó hoành độ điểm M là 30.
⇒ \(\;\sin \alpha {\rm{ }} = \;\frac{{MH}}{{OM}} = \;\frac{{30}}{{31}}\)
\( \Rightarrow \cos \alpha = \sqrt {1 - {{\left( {\frac{{30}}{{31}}} \right)}^2}} = \frac{{\sqrt {61} }}{{31}}\)
b, Vì các cánh quạt tạo thành 3 góc bằng nhau nên \(\widehat {MOP} = \widehat {NOP} = \widehat {MON} = {120^0}\)
\( \Rightarrow \widehat {AOP} = \widehat {MOP} - \widehat {MOA}\)
\( \Leftrightarrow \sin \widehat {AOP} = \sin \left( {\widehat {MOP} - \widehat {MOA}} \right) = \sin \widehat {MOP}.\cos \widehat {MOA} - \cos \widehat {MOP}.\sin \widehat {MOA}\)
\( = \sin \frac{{2\pi }}{3}.\cos \alpha - \cos \frac{{2\pi }}{3}.\sin \alpha \approx 0,7\)
Vì vậy chiều cao của điểm P so với mặt đất là:
31. \(\sin \widehat {AOP}\) + 60 = 31.0,7+ 60 \( \approx \) 81,76 m.
Ta có:
\(\cos \widehat {AOP} \approx \sqrt {1 - 0,{7^2}} = 0,71\)
\(\widehat {AON} = \widehat {AOP} + \widehat {PON}\)
\(\begin{array}{l} \Leftrightarrow \sin \widehat {AON} = \sin \left( {\widehat {AOP} + \widehat {PON}} \right)\\ \Leftrightarrow \sin \widehat {AON} = \sin \widehat {AOP}.\cos \widehat {PON} + \cos \widehat {AOP}.\sin \widehat {PON}\\ \Leftrightarrow \sin \widehat {AON} = 0,7.\cos \frac{{2\pi }}{3} + 0,71.\sin \frac{{2\pi }}{3} \approx 0,26\end{array}\)
\( \Rightarrow \sin \left( {OA,ON} \right) = \sin \widehat {AON} \approx 0,26\)
Vì vậy chiều cao của điểm N so với mặt đất là:
31. \(\sin \widehat {AON}\) + 60 = 31.0,26+ 60\( \approx \) 68,2 m.

Thanh OM quay được \(3\dfrac{1}{10}\) vòng thì \(\alpha=3\dfrac{1}{10}\cdot360^o=1116^o\)
Từ M kẻ MH \(\perp\) Ox
\(\Rightarrow OH=15\cdot\left|cos1116^o\right|\approx12,1\)
Vậy độ dài bóng O'M' của OM khi thanh quay được \(3\dfrac{1}{10}\) là 12,1cm.

a) M(-1;1) đối xứng qua trục Oy ta được N(-1;1).
Gọi M'(x;y) là ảnh của N(-1;1) qua phép tịnh tiến theo vectơ v → = ( 2 ; 0 )
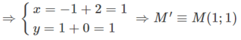
b) Gọi P(x;y) là ảnh của M(1;1) qua phép tịnh tiến theo v → = ( 2 ; 0 )
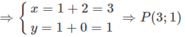
P(3;1) đối xứng qua trục Oy ta được M"(-3;1)

Khi: \(s = - 5\sqrt 3 \;\)thì \(10sin\left( {10t + \frac{\pi }{2}} \right) = - 5\sqrt 3 \; \Leftrightarrow sin\left( {10t + \frac{\pi }{2}} \right) = - \frac{{\sqrt 3 }}{2}\)
\(\begin{array}{l} \Leftrightarrow sin\left( {10t + \frac{\pi }{2}} \right) = \sin \left( { - \frac{\pi }{3}} \right)\\ \Leftrightarrow \left[ \begin{array}{l}10t + \frac{\pi }{2} = - \frac{\pi }{3} + k2\pi \\10t + \frac{\pi }{2} = \pi + \frac{\pi }{3} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}t = - \frac{\pi }{{12}} + k\frac{\pi }{5}\\t = \frac{\pi }{{12}} + k\frac{\pi }{5}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\)
Vậy \(t = \pm \frac{\pi }{{12}} + k\frac{\pi }{5},k \in \mathbb{Z}\) là giá trị cần tìm.

Tham khảo:
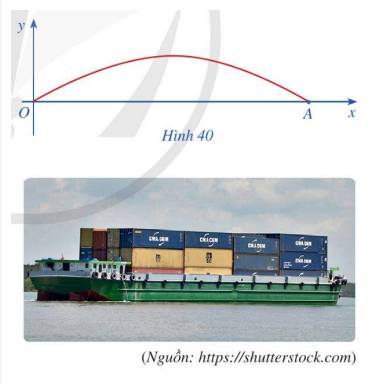
a) Hai vị trí \(O\) và \(A\) là hai vị trí chân cầu, tại hai vị trí này ta có: \(y = 0\)
\( \Leftrightarrow 4,8 \cdot \sin \frac{x}{9} = 0 \Leftrightarrow \sin \frac{x}{9} = 0 \Leftrightarrow \frac{x}{9} = k\pi (k \in \mathbb{Z}) \Leftrightarrow x = 9k\pi (k \in \mathbb{Z})\)
Quan sát đồ thị ta thấy, đồ thị hàm số \({\rm{y}} = 4,8 \cdot \sin \frac{x}{9}\) cắt trục hoành tại điểm 0 và \({\rm{A}}\) liên tiếp nhau với \(x \ge 0\).
Xét \({\rm{k}} = 0\), ta có \({{\rm{x}}_1} = 0\);
Xét \({\rm{k}} = 1\), ta có \({{\rm{x}}_2} = 9\pi \).
Mà \({x_1} = 0\) nên đây là hoành độ của 0 , do đó \({x_2} = 9\pi \) là hoành độ của điểm \(A\).
Khi đó \(OA = 9\pi \approx 28,3\).
Vậy chiều rộng của con sông xấp xỉ 28,3 m.
b) Do sà lan có độ cao 3,6 m so với mực nước sông nên khi sà lan đi qua gầm cầu thì ứng với \({\rm{y}} = 3,6\).
\( \Leftrightarrow 4,8 \cdot \sin \frac{x}{9} = 3,6 \Leftrightarrow \sin \frac{x}{9} = \frac{3}{4} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{\frac{{\rm{x}}}{9} \approx 0,848 + {\rm{k}}2\pi }\\{\frac{{\rm{x}}}{9} \approx \pi - 0,848 + {\rm{k}}2\pi }\end{array}} \right.\)
(Dùng máy tính cầm tay (chuyển về chế độ “radian”) bấm liên tiếp \(SHIFT\)\sin 3 \div 4 = ta được kết quả gần đúng là 0,85) \( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{{\rm{x}} \approx 7,632 + 18{\rm{k}}\pi }\\{{\rm{x}} \approx 9\pi - 7,632 + 18{\rm{k}}\pi }\end{array}({\rm{k}} \in \mathbb{Z})} \right.\)
Xét \({\rm{k}} = 0\), ta có \({{\rm{x}}_1} \approx 7,632;{{\rm{x}}_2} \approx 20,642\).
Ta biểu diễn các giá trị \(x\) vừa tìm được trên hệ trục tọa độ vẽ đồ thị hàm số \(y = \) 4,8. \(\sin \frac{x}{9}\) như sau:
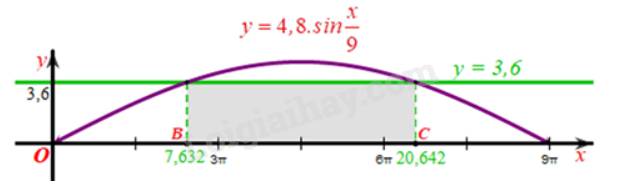
Khi đó để sà lan có thể đi qua được gầm cầu thì khối hàng hóa có độ cao 3,6 m phải có chiều rộng nhỏ hơn độ dài đoạn thẳng \({\rm{BC}}\) trên hình vẽ.
Mà \(BC \approx 20,642 - 7,632 = 13,01(m) < 13,1(m)\).
Vậy chiều rộng của khối hàng hoá đó phải nhỏ hơn 13,1 m.
c) Giả sử sà lan chở khối hàng được mô tả bởi hình chữ nhật MNPQ:
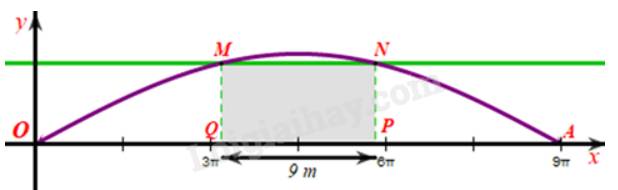
Khi đó \(QP = 9;OA = 28,3\) và \(OQ = PA\).
Mà \(OQ + QP + PA = OA \Rightarrow OQ + 9 + OQ \approx 28,3 \Rightarrow OQ \approx 9,65\)
Khi đó \({y_M} = 4,8 \cdot \sin \frac{{{x_M}}}{9} = 4,8 \cdot \sin \frac{{OQ}}{9} \approx 4,8 \cdot \sin \frac{{9,65}}{9} \approx 4,22(\;{\rm{m}}) < 4,3\) (m).
Vậy để sà lan có thể đi qua được gầm cầu thì chiều cao của khối hàng hoá đó phải nhỏ hơn 4,3 m.
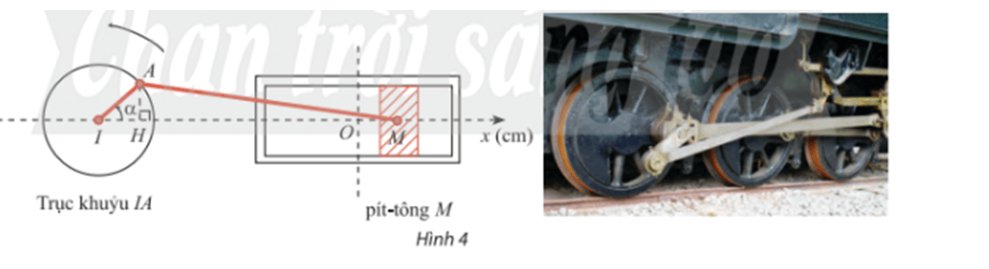

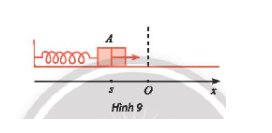
a, Tại \(\alpha = \frac{\pi }{2}\) thì H trùng I, M trùng O nên MH = OI do đó OM = IH.
Xét tam giác AHI vuông tại H có: \(IH = cos\alpha .IA = 8cos\alpha .\)
\( \Rightarrow {x_M} = OM = IH = 8cos\alpha \)
b, Sau khi chuyển động được 1 phút, trục khuỷu quay được một góc là \(\alpha \)
Khi đó \({x_M} = - 3cm \Rightarrow cos\alpha = - \frac{3}{8}\)
Sau khi chuyển động 2 phút, trục khuỷu quay được một góc \(2\alpha \), nên:
\({x_M} = 8cos2\alpha = 8\left( {2{{\cos }^2}\alpha - 1} \right)\)\( = 8\left( {2{{\left( { - \frac{3}{8}} \right)}^2} - 1} \right) \approx - 5,8 cm\)