Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đồ thị hàm số lẻ nhận gốc tọa độ làm tâm đối xứng nên phương án B đúng.

Đáp án D
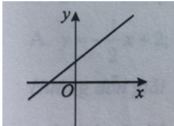
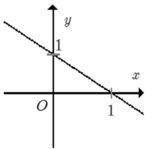
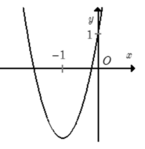
Đồ thị đi xuống từ trái sang phải => hệ số góc a < 0. Loại A, C.
Đồ thị hàm số cắt trục tung tại điểm (0; 1).

Đáp án D
Nhận xét:
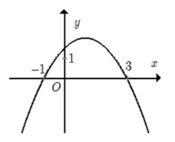
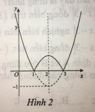
Parabol có bề lõm hướng xuống. Loại đáp án A, C.
Parabol cắt trục hoành tại 2 điểm (3; 0) và (−1; 0). Xét các đáp án B và D, đáp án D thỏa mãn.

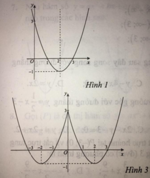
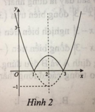
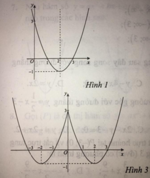
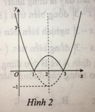
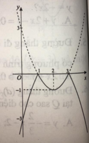
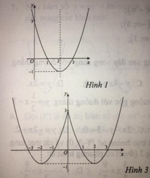
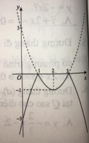
Hàm số y = x 2 - 4 x + 3 là hàm số chẵn nhận trục Oy làm trục đối xứng nên chỉ có hình 3 thỏa mãn .

Ta có: y = x 2 - 4 x + 3 = x 2 - 4 x + 3 k h i x 2 - 4 x + 3 ≥ 0 - x 2 - 4 x + 3 k h i x 2 - 4 x + 3 < 0
Cách vẽ đồ thị y = x 2 - 4 x + 3
+ Vẽ đồ thị hàm số y = x2 – 4x + 3 (C).
+ Giữ nguyên phần đồ thị (C) phía trên trục hoành
Lấy đối xứng phần dưới trục hoành qua trục hoành; xóa phần đồ thị (C) dưới trục hoành.
Khi đó, ta được đồ thị hàm số y = x 2 - 4 x + 3 .
Chọn B

Đồ thị của hàm số y = x2 – 4x + 3 là đường cong parabol nên chọn A.

Đáp án :
B. Đồ thị hàm số chẵn nhận trục hoành làm trục đối xứng.

Đáp án: B
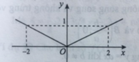
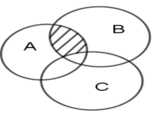
Phần bị gạch là phần thuộc (A ∩ B) nhưng không thuộc C nên phần bị gạch biểu thị cho (A ∩ B) \ C.
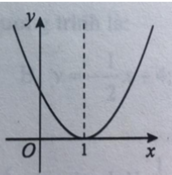

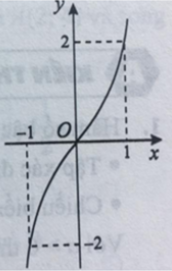
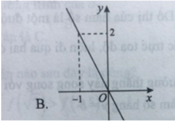
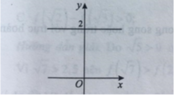
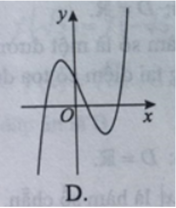


Vì đồ thị hàm số chẵn nhận trục tung làm trục đối xứng nên phương án C đúng.