
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 170:
Gọi $H(a,b)$ là tọa độ trực tâm của tam giác $ABC$
Có:
$AH\perp BC$
$\Leftrightarrow \overrightarrow{AH}.\overrightarrow{BC}=0$
$\Leftrightarrow (a+3, b-6).(-14,14)=0$
$\Leftrightarrow -14(a+3)+14(b-6)=0$
$\Leftrightarrow -a-3+b-6=0$
$\Leftrightarrow -a+b=9(1)$
$BH\perp AC$
$\Leftrightarrow \overrightarrow{BH}.\overrightarrow{AC}=0$
$\Leftrightarrow (a-9, b+10).(-2, -2)=0$
$\Leftrightarrow -2(a-9)-2(b+10)=0$
$\Leftrightarrow a-9+b+10=0$
$\Leftrightarrow a+b=-1(2)$
Từ $(1); (2)\Rightarrow a=-5; b=4$
Đáp án C.
Câu 189:
Gọi $I(a,b)$ là tâm đường tròn ngoại tiếp tam giác $ABC$.
$M(\frac{3}{2}, \frac{-1}{2}), N(\frac{5}{2}, \frac{1}{2})$ lần lượt là trung điểm của $AB, BC$
Có:
$IM\perp AB$
$\Leftrightarrow \overrightarrow{MI}.\overrightarrow{AB}=0$
$\Leftrightarrow (a-\frac{3}{2}, b+\frac{1}{2}).(-1, -3)=0$
$\Leftrightarrow -(a-\frac{3}{2})-3(b+\frac{1}{2})=0$
$\Leftrightarrow a-\frac{3}{2}+3b+\frac{3}{2}=0$
$\Leftrightarrow a+3b=0(1)$
Lại có:
$IN\perp BC$
$\Leftrightarrow \overrightarrow{NI}.\overrightarrow{BC}=0$
$\Leftrightarrow (a-\frac{5}{2}, b-\frac{1}{2})(3,5)=0$
$\Leftrightarrow 3(a-\frac{5}{2})+5(b-\frac{1}{2})=0$
$\Leftrightarrow 3a+5b=10(2)$
Từ $(1); (2)\Rightarrow a=\frac{15}{2}; b=\frac{-5}{2}$
Đáp án A.



Câu 1:
\(\left\{{}\begin{matrix}y-2x< =2\\2y-x>=4\\x+y< =5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y< =2x+2\\2y>=x+4\\y< =-x+5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y< =2x+2\\y< =-x+5\\y>=\dfrac{1}{2}x+2\end{matrix}\right.\)
y<=2x+2
=>y-2x-2<=0
Vẽ đường thẳng y=2x+2
Khi x=0 và y=0 thì \(y-2x-2=0-0-2=-2< =0\)(đúng)
=>Miền nghiệm của BPT y<=2x+2 là nửa mặt phẳng vừa chứa biên vừa chứa điểm O(0;0)
y<=-x+5
=>x+y-5<=0
Khi x=0 và y=0 thì \(x+y-5=0+0-5< =0\)(đúng)
=>Miền nghiệm của BPT y<=-x+5 là nửa mặt phẳng vừa chứa biên vừa chứa điểm O(0;0)
y>=1/2x+2
=>\(-\dfrac{1}{2}x+y-2>=0\)
Khi x=0 và y=0 thì \(-\dfrac{1}{2}x+y-2=-\dfrac{1}{2}\cdot0+0-2=-2< 0\)
=>O(0;0) không thỏa mãn BPT \(-\dfrac{1}{2}x+y-2>=0\)
=>Miền nghiệm của BPT \(y>=\dfrac{1}{2}x+2\) là nửa mặt phẳng chứa biên nhưng không chứa điểm O(0;0)
Vẽ đồ thị:
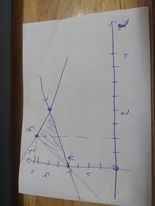
Theo hình vẽ, ta có: Miền nghiệm của hệ BPT sẽ là ΔABC, với A(0;2); B(1;4); C(2;3)
Khi x=0 và y=2 thì F=2-0=2
Khi x=1 và y=4 thì F=4-1=3
Khi x=2 và y=3 thì F=3-2=1
=>Chọn A

15.
\(\Delta'=m^2+m-2>0\Leftrightarrow\left[{}\begin{matrix}m>1\\m< -2\end{matrix}\right.\)
Đáp án B
16.
\(\dfrac{\pi}{2}< a< \pi\Rightarrow\dfrac{\pi}{4}< \dfrac{a}{2}< \dfrac{\pi}{2}\Rightarrow\dfrac{\sqrt{2}}{2}< sin\dfrac{a}{2}< 1\Rightarrow\dfrac{1}{2}< sin^2\dfrac{a}{2}< 1\)
\(sina=\dfrac{3}{5}\Leftrightarrow sin^2a=\dfrac{9}{25}\Leftrightarrow4sin^2\dfrac{a}{2}.cos^2\dfrac{a}{2}=\dfrac{9}{25}\)
\(\Leftrightarrow sin^2\dfrac{a}{2}\left(1-sin^2\dfrac{a}{2}\right)=\dfrac{9}{100}\Leftrightarrow sin^4\dfrac{a}{2}-sin^2\dfrac{a}{2}+\dfrac{9}{100}=0\)
\(\Rightarrow\left[{}\begin{matrix}sin^2\dfrac{a}{2}=\dfrac{1}{10}< \dfrac{1}{2}\left(loại\right)\\sin^2\dfrac{a}{2}=\dfrac{9}{10}\end{matrix}\right.\)
\(\Rightarrow sin\dfrac{a}{2}=\dfrac{3\sqrt{10}}{10}\)
17.
Áp dụng công thức trung tuyến:
\(AM=\dfrac{\sqrt{2\left(AB^2+AC^2\right)-BC^2}}{2}=\dfrac{\sqrt{201}}{2}\)
18.
\(\Leftrightarrow x^2+2x+4>m^2+2m\) ; \(\forall x\in\left[-2;1\right]\)
\(\Leftrightarrow m^2+2m< \min\limits_{\left[-2;1\right]}\left(x^2+2x+4\right)\)
Xét \(f\left(x\right)=x^2+2x+4\) trên \(\left[-2;1\right]\)
\(-\dfrac{b}{2a}=-1\in\left[-2;1\right]\) ; \(f\left(-2\right)=4\) ; \(f\left(-1\right)=3\) ; \(f\left(1\right)=7\)
\(\Rightarrow\min\limits_{\left[-2;1\right]}\left(x^2+2x+4\right)=f\left(1\right)=3\)
\(\Rightarrow m^2+2m< 3\Leftrightarrow m^2+2m-3< 0\)
\(\Rightarrow-3< m< 1\Rightarrow m=\left\{-2;-1;0\right\}\)
Đáp án C

Câu 10 sai, đáp án B đúng, sử dụng đan dấu trên trục số dễ dàng thấy:

12. Câu này sai, A mới đúng. Đơn giản là em nhìn kĩ lại công thức lượng giác là thấy thôi, nhầm lẫn về hệ số trong công thức biến tích thành tổng
\(cosa.cosb=\dfrac{1}{2}....\)
14. Đáp án C đúng
\(\overrightarrow{BA}=\left(2;2\right)=2\left(1;1\right)\) nên trung trực AB nhận (1;1) là 1 vtpt
Gọi M là trung điểm AB \(\Rightarrow M\left(0;2\right)\)
Phương trình: \(1\left(x-0\right)+1\left(y-2\right)=0\Leftrightarrow x+y-2=0\)
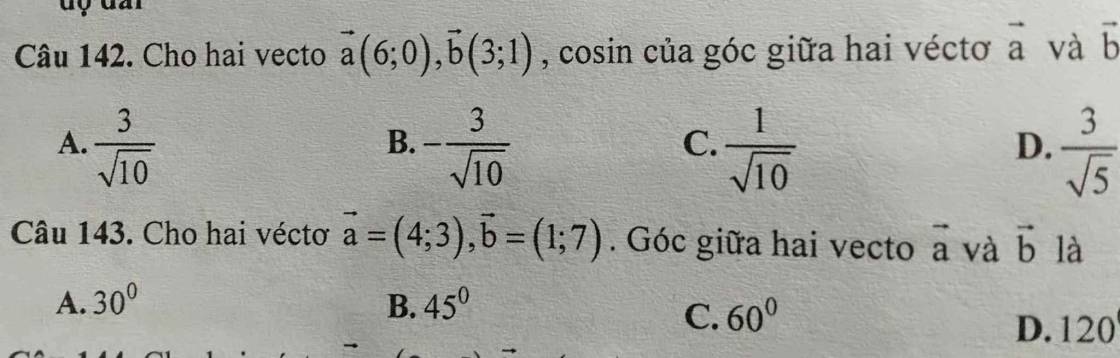


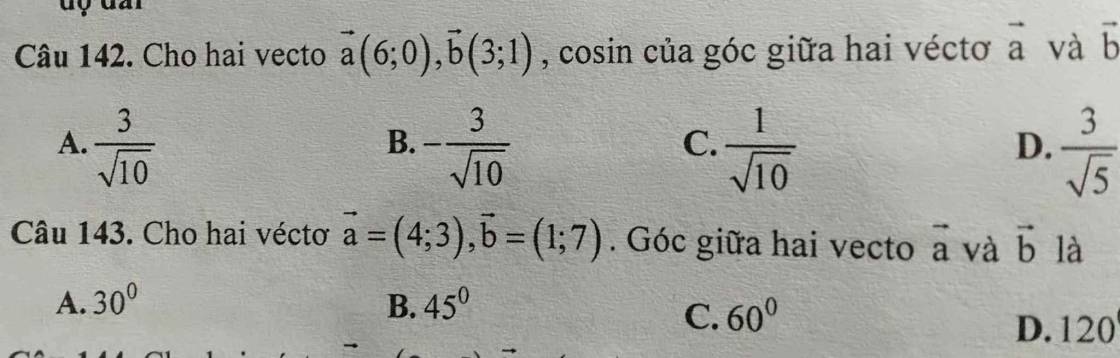
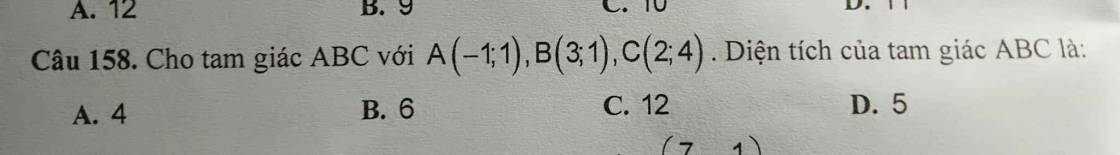
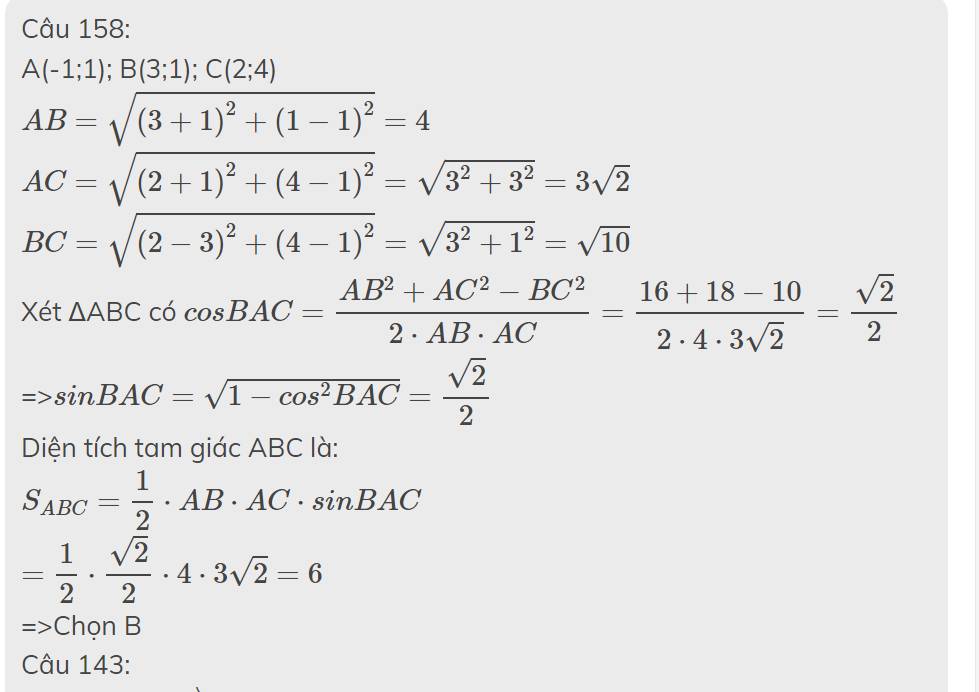
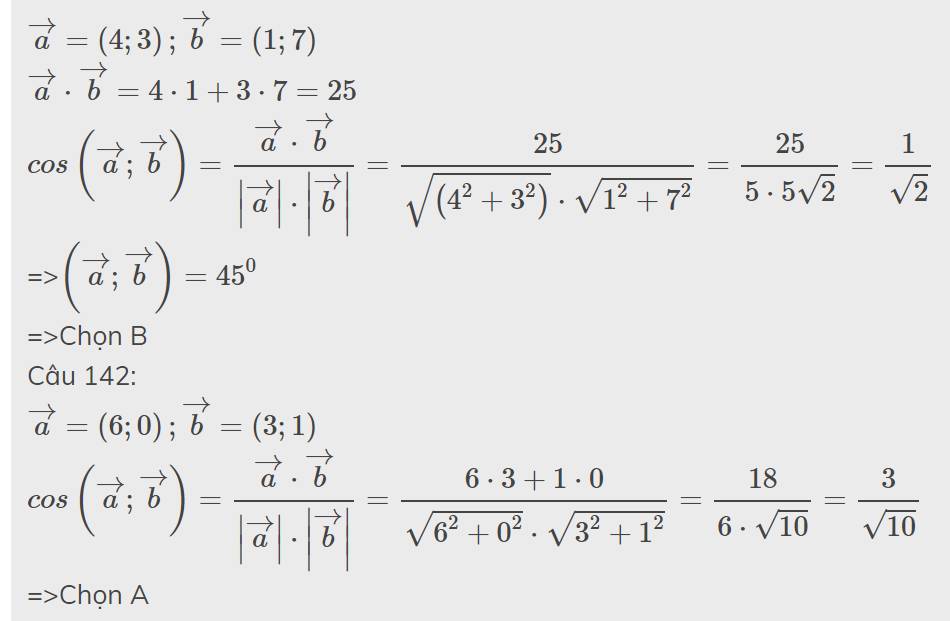
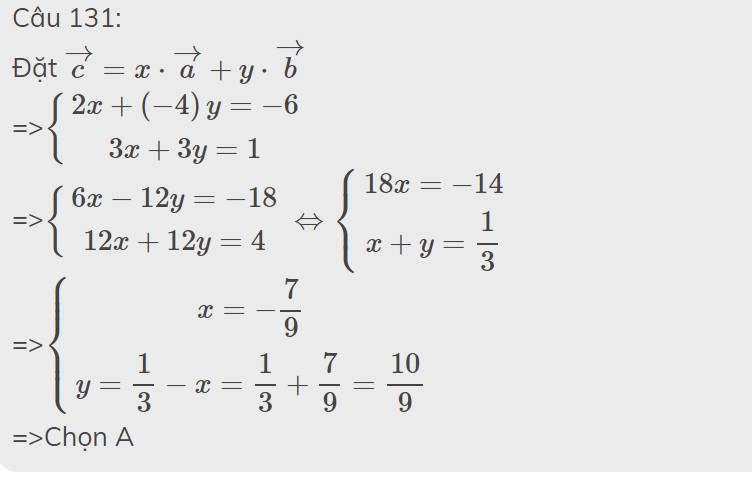
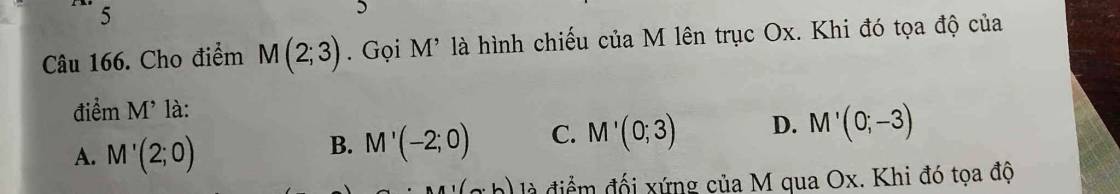
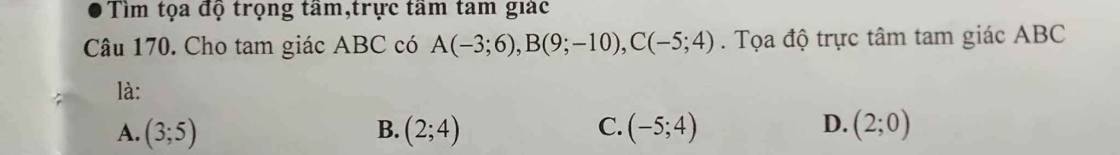
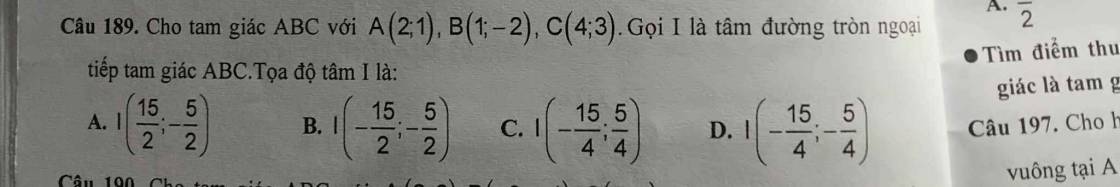









Câu 158:
A(-1;1); B(3;1); C(2;4)
\(AB=\sqrt{\left(3+1\right)^2+\left(1-1\right)^2}=4\)
\(AC=\sqrt{\left(2+1\right)^2+\left(4-1\right)^2}=\sqrt{3^2+3^2}=3\sqrt{2}\)
\(BC=\sqrt{\left(2-3\right)^2+\left(4-1\right)^2}=\sqrt{3^2+1^2}=\sqrt{10}\)
Xét ΔABC có \(cosBAC=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=\dfrac{16+18-10}{2\cdot4\cdot3\sqrt{2}}=\dfrac{\sqrt{2}}{2}\)
=>\(sinBAC=\sqrt{1-cos^2BAC}=\dfrac{\sqrt{2}}{2}\)
Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\cdot sinBAC\)
\(=\dfrac{1}{2}\cdot\dfrac{\sqrt{2}}{2}\cdot4\cdot3\sqrt{2}=6\)
=>Chọn B
Câu 143:
\(\overrightarrow{a}=\left(4;3\right);\overrightarrow{b}=\left(1;7\right)\)
\(\overrightarrow{a}\cdot\overrightarrow{b}=4\cdot1+3\cdot7=25\)
\(cos\left(\overrightarrow{a};\overrightarrow{b}\right)=\dfrac{\overrightarrow{a}\cdot\overrightarrow{b}}{\left|\overrightarrow{a}\right|\cdot\left|\overrightarrow{b}\right|}=\dfrac{25}{\sqrt{\left(4^2+3^2\right)}\cdot\sqrt{1^2+7^2}}=\dfrac{25}{5\cdot5\sqrt{2}}=\dfrac{1}{\sqrt{2}}\)=>\(\left(\overrightarrow{a};\overrightarrow{b}\right)=45^0\)
=>Chọn B
Câu 142:
\(\overrightarrow{a}=\left(6;0\right);\overrightarrow{b}=\left(3;1\right)\)
\(cos\left(\overrightarrow{a};\overrightarrow{b}\right)=\dfrac{\overrightarrow{a}\cdot\overrightarrow{b}}{\left|\overrightarrow{a}\right|\cdot\left|\overrightarrow{b}\right|}=\dfrac{6\cdot3+1\cdot0}{\sqrt{6^2+0^2}\cdot\sqrt{3^2+1^2}}=\dfrac{18}{6\cdot\sqrt{10}}=\dfrac{3}{\sqrt{10}}\)
=>Chọn A
Câu 131:
Đặt \(\overrightarrow{c}=x\cdot\overrightarrow{a}+y\cdot\overrightarrow{b}\)
=>\(\left\{{}\begin{matrix}2x+\left(-4\right)y=-6\\3x+3y=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}6x-12y=-18\\12x+12y=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}18x=-14\\x+y=\dfrac{1}{3}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-\dfrac{7}{9}\\y=\dfrac{1}{3}-x=\dfrac{1}{3}+\dfrac{7}{9}=\dfrac{10}{9}\end{matrix}\right.\)
=>Chọn A