Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ΔODB và ΔOCA có
\(\dfrac{OD}{OC}=\dfrac{OB}{OA}\left(\dfrac{3}{6}=\dfrac{4}{8}\right)\)
\(\widehat{O}\) chung
Do đó: ΔODB đồng dạng với ΔOCA
=>\(\dfrac{OD}{OC}=\dfrac{OB}{OA}\)
=>\(\dfrac{OD}{OB}=\dfrac{OC}{OA}\)
Xét ΔODC và ΔOBA có
\(\dfrac{OD}{OB}=\dfrac{OC}{OA}\)
\(\widehat{O}\) chung
Do đó: ΔODC đồng dạng với ΔOBA
=>\(\dfrac{DC}{BA}=\dfrac{OC}{OA}\)
=>\(\dfrac{DC}{5}=\dfrac{6}{8}=\dfrac{3}{4}\)
=>\(DC=3\cdot\dfrac{5}{4}=\dfrac{15}{4}=3,75\left(cm\right)\)

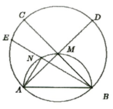
Các tam giác ∆ANE, ∆AMC và ∆BMD vuông cân
=> A E B ^ = A D B ^ = A C B ^ = 45 0
Mà AB cố định nên các điểm A, B, C, D, E cùng thuộc một đường tròn

*Kẻ OI ⊥ EM, OH ⊥ FM. (1)
Theo đề, ta có AB=CD, AE=BM, CF=DM
Mà AI+EA=EI, IB+BM=IB và MD+DH=MH, HC+CF=HF
=>EM=MF (2)
Từ (1) và (2), suy ra:
IO=OH (định lí giữa dây và khoảng cách từ tâm đến dây)(3)
EI=IM, MH=HF(định lí đường kính và dây) => EI=IM=MH= HF (4)
Xét △EOI và △FOH, có:
EI=FH (theo (4)) , góc EIO= góc FHO (=90o)
IO=OH (theo(3))
=> △EIO=△FOH (c.g.c)
Do đó: OE=OF ( 2 cạnh tương ứng)
Vậy OE=OF (đpcm)
HAVE A GOOD DAY!
a, vì OB<OA(6<11)
=> B nằm giữa O;A
b, vì B nằm giữa O;A
Nên ta có :
OB+AB=OA
=> 6+AB=11
=> AB= 5(cm)
c, vì C thuộc tia đối Ox=> O nằm giữa C;B
ta có : OC+OB=BC
=> 5+6=BC
=> BC=11(cm)
hình bn tự vẽ nhé
Trên tia Ox chứ có phải là tia õ đâu!!!!!!!!!!!!!!!!!
Mà bài này lớp 9 hay 6 vậy????