Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
Số hạt dẻ trên mỗi ô (bắt đầu từ ô thứ nhất) theo thứ tự đó lập thành cấp số cộng có u1 = 7; d = 5 .
Gọi n là số ô trên bàn cờ thì u1 + u2 + L + un = 25450 = Sn
Ta có 25450 = Sn = ![]() 5n2 + 9n – 50900 = 0
5n2 + 9n – 50900 = 0
Hay n = 100.

Đáp án D
Gọi ô chứa hạt thóc thỏa mãn đề bài là ô thứ n ( n ∈ N , n > 1 ) . Khi đó


Số hạt thóc ở các ô từ ô thứ nhất đến thứ sáu: 1; 2; 4; 8; 16; 32

Ta có:
S = u1 + u2 + u3 + u4 + u5 + u6 + u7 + u8 + u9 + u10 + u11
= u1 + u1.q + u1.q2 +⋯+ u1.q9 + u1.q10 (1)
⇒ S.q = u1.q + u1.q2 +⋯+ u1.q9 + u1.q10 + u1.q11 (2)
Lấy (1) trừ (2), ta được:
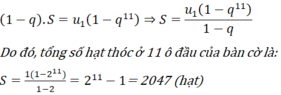

2, sin4x+cos5=0 <=> cos5x=cos\(\left(\frac{\pi}{2}+4x\right)\Leftrightarrow\orbr{\begin{cases}x=\frac{\pi}{2}+k2\pi\\x=-\frac{\pi}{18}+\frac{k2\pi}{9}\end{cases}\left(k\inℤ\right)}\)
ta có \(2\pi>0\Leftrightarrow k< >\frac{1}{4}\)do k nguyên nên nghiệm dương nhỏ nhất trong họ nghiệm \(\frac{\pi}{2}\)khi k=0
\(-\frac{\pi}{18}+\frac{k2\pi}{9}>0\Leftrightarrow k>\frac{1}{4}\)do k nguyên nên nghiệm dương nhỏ nhất trong họ nghiệm \(-\frac{\pi}{18}-\frac{k2\pi}{9}\)là \(\frac{\pi}{6}\)khi k=1
vậy nghiệm dương nhỏ nhất của phương trình là \(\frac{\pi}{6}\)
\(\frac{\pi}{2}+k2\pi< 0\Leftrightarrow k< -\frac{1}{4}\)do k nguyên nên nghiệm âm lớn nhất trong họ nghiệm \(\frac{\pi}{2}+k2\pi\)là \(-\frac{3\pi}{2}\)khi k=-1
\(-\frac{\pi}{18}+\frac{k2\pi}{9}< 0\Leftrightarrow k< \frac{1}{4}\)do k nguyên nên nghiệm âm lớn nhất trong họ nghiệm \(-\frac{\pi}{18}+\frac{k2\pi}{9}\)là \(-\frac{\pi}{18}\)khi k=0
vậy nghiệm âm lớn nhất của phương trình là \(-\frac{\pi}{18}\)

Số hạt dẻ trên mỗi ô (bắt đầu từ ô thứ nhất) theo thứ tự đó lập thành cấp số cộng ( u n ) có u 1 = 7 , d = 5.
Gọi n là số ô trên bàn cờ thì u 1 + u 2 + ⋯ + u n = 25450 = S n .
Ta có 25450 = S n = n u 1 + n n − 1 2 d = 7 n + n 2 − n 2 .5
⇔ 5 n 2 + 9 n − 50900 = 0 ⇔ n = 100
Chọn đáp án B