Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Toán lớp 10 Chương 3: PHƯƠNG TRÌNH, HỆ PHƯƠNG TRÌNH §2. Phương trình quy về phương trình bậc nhất, bậc hai

Người duyệt vào duyệt lại về trạng thái chưa duyệt thì sẽ xoá và sửa đc

a, Gọi \(I\left(x;y\right)\) là tâm đường tròn ngoại tiếp \(\Delta ABC\)
\(\Rightarrow\left\{{}\begin{matrix}IA=IB\\IA=IC\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}IA^2=IB^2\\IA^2=IC^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(-3-x\right)^2+\left(6-y\right)^2=\left(1-x\right)^2+\left(-2-y\right)^2\\\left(-3-x\right)^2+\left(6-y\right)^2=\left(6-x\right)^2+\left(3-y\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-2y=-5\\3x-y=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=3\end{matrix}\right.\)

Đáp án B
![]() => Đường thẳng AB có pt là: x- y – 5= 0.
=> Đường thẳng AB có pt là: x- y – 5= 0.
Gọi G(a;3a- 8) suy ra C( 3a- 5; 9a -19).
Ta có:

Vậy C( 1 ; -1) và C( -2 ; 10)

Từ phương trình \(\Rightarrow a^2=25\Rightarrow a=5\)
Độ dài trục lớn: \(2a=10\)

Đáp án B
Gọi hình bình hành là ABCD và
d:x+ y-1 = 0, ∆: 3x – y+ 5= 0 .
Không làm mất tính tổng quát giả sử
![]()
Ta có : ![]() . Vì I(3;3) là tâm hình bình hành nên C(7;4) ;
. Vì I(3;3) là tâm hình bình hành nên C(7;4) ; ![]()
=> Đường thẳng ACcó pt là: x- 4y + 9= 0.
Do ![]() => Đường thẳng BC đi qua điểm C và có vtpt
=> Đường thẳng BC đi qua điểm C và có vtpt ![]() có pt là: 3x – y- 17= 0.
có pt là: 3x – y- 17= 0.
Khi đó :
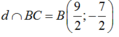
Ta có:
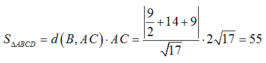

Câu 2:
y=f(x)=3x +1
4 = 3x +1
3x +1 = 4
3x = 4 - 1
3x = 3
x = 3 : 3
x = 1

Đơn giản nhất là bình phương lên:
Đặt \(A=\left|2\overrightarrow{i}+2\overrightarrow{j}\right|\Rightarrow A^2=4\overrightarrow{i}^2+4\overrightarrow{j}^2+8\overrightarrow{i}.\overrightarrow{j}\)
Với chú ý rằng \(\overrightarrow{i};\overrightarrow{j}\) là các vecto đơn vị nên \(\overrightarrow{i}\perp\overrightarrow{j}\) và độ dài của chúng đều bằng 1
\(\Rightarrow A^2=4+4+0=8\Rightarrow A=2\sqrt{2}\)
\(\overrightarrow{i}\perp\overrightarrow{j}\Rightarrow\overrightarrow{i}.\overrightarrow{j}=0\) tính chất cơ bản của tích vô hướng