Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

* Gọi phương trình đường thẳng AB là y = ax + b.
Tọa độ các điểm A, B phải thỏa mãn phương trình y = ax + b nên ta có:
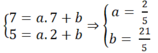
Vậy phương trình của đường thẳng AB là y = 2/5x + 21/5.
*Gọi phương trình của đường thẳng BC là y = a’x + b’.
Tương tự như trên ta có:
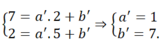
Vậy phương trình của đường thẳng BC là y = -x + 7.
*Gọi phương trình của đường thẳng AC là y = a’’x + b’’.
Tương tự như trên ta có: 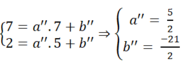
Vậy phương trình của đường thẳng AC là y = 5/2x - 21/2.

a: vecto AB=(-2;-3)=(2;3)
=>VTPT là (-3;2)
Phương trình đường thẳng AB là:
-3(x-0)+2(y-3)=0
=>-3x+2y-6=0
=>3x-2y+6=0
vecto AC=(2;-3)
=>VTPT là (3;2)
Phương trình AC là:
3(x-2)+2(y-0)=0
=>3x+2y-6=0
vecto BC=(4;0)
=>vtpt là (0;-4)
Phương trình BC là;
0(x-2)+(-4)(y-0)=0
=>-4y=0
=>y=0
b: \(AB=\sqrt{\left(-2\right)^2+3^2}=\sqrt{13}\)
\(AC=\sqrt{\left(2-0\right)^2+\left(0-3\right)^2}=\sqrt{13}\)
\(BC=\sqrt{\left(2+2\right)^2+\left(0-0\right)^2}=4\)
\(C_{ABC}=\sqrt{13}+\sqrt{13}+4=4+2\sqrt{13}\)
\(cosBAC=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=\dfrac{13+13-4^2}{2\cdot\sqrt{13}\cdot\sqrt{13}}=\dfrac{5}{13}\)
=>sin BAC=căn 1-(5/13)^2=căn 144/169=12/13
\(S_{BAC}=\dfrac{1}{2}\cdot AB\cdot AC\cdot\dfrac{12}{13}=\dfrac{12}{13}\cdot13=12\)

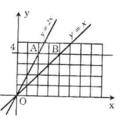
a) Vẽ đồ thị:
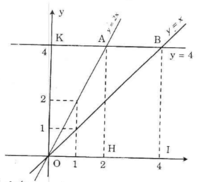
b) - Từ hình vẽ ta có: yA = yB = 4 suy ra:.
+ Hoành độ của A: 4 = 2.xA => xA = 2 (*)
+ Hoành độ của B: 4 = xB => xB = 4
=> Tọa độ 2 điểm là: A(2, 4); B(4, 4)
- Tìm độ dài các cạnh của ΔOAB
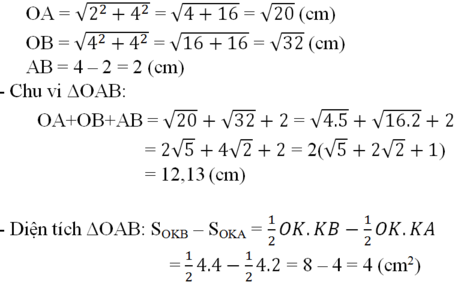
((*): muốn tìm tung độ hay hoành độ của một điểm khi đã biết trước hoành độ hay tung độ, ta thay chúng vào phương trình đồ thị hàm số để tìm đơn vị còn lại.)

a) - Với hàm số y = x + 1:
Cho x = 0 => y = 1 ta được M(0; 1).
Cho y = 0 => x + 1 = 0 => x = -1 ta được B(-1; 0).
Nối MB ta được đồ thị hàm số y = x + 1.
- Với hàm số y = -x + 3:
Cho x = 0 => y = 3 ta được E(0; 3).
Cho y = 0 => -x + 3 = 0 => x = 3 ta được A(3; 0).
Nối EA ta được đồ thị hàm số y = -x + 3.
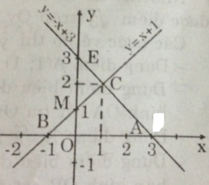
b) Từ hình vẽ ta có:
- Đường thẳng y = x + 1 cắt Ox tại B(-1; 0).
- Đường thẳng y = -x + 3 cắt Ox tại A(3; 0).
- Hoành độ giao điểm C của 2 đồ thị hàm số y = x + 1 và y = -x + 3 là nghiệm phương trình:
x + 1 = -x + 3
=> x = 1 => y = 2
=> Tọa độ C(1; 2)
c) Ta có: AB = 3 + 1 = 4
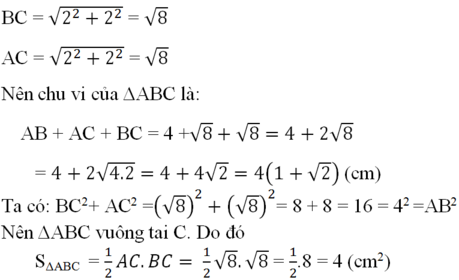

a) Vẽ đường thẳng y = -x + 2
Cho x = 0 => y = 2 được C(0; 2)
Cho y = 0 => x = 2 được A(2; 0)
Nối A, C ta được đường thẳng y = -x + 2
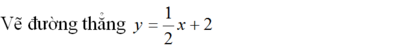
Cho x = 0 => y = 2 được C(0; 2)
Cho y = 0 => x = -4 được B(-4; 0)
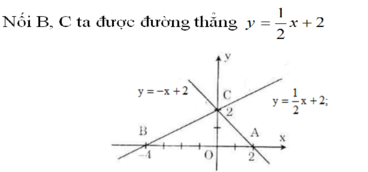

c) Áp dụng định lí Pitago ta có:
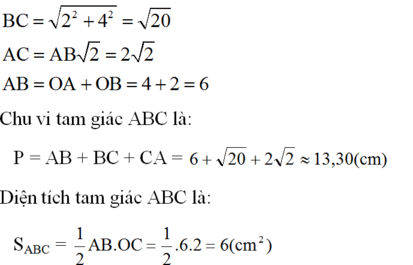

a) Vẽ đường thẳng qua O(0; 0) và điểm M(1; 1) được đồ thị hàm số y = x.
Vẽ đường thẳng qua B(0; 2) và A(-2; -2) được đồ thị hàm số y = 2x + 2.
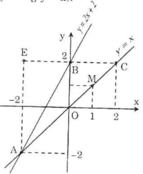
b) Hoành độ giao điểm của 2 đồ thị hàm số là nghiệm của phương trình:
2x + 2 = x
=> x = -2 => y = -2
Suy ra tọa độ giao điểm là A(-2; -2).
c) Qua B(0; 2) vẽ đường thẳng song song với Ox, đường thẳng này có phương trình y = 2 và cắt đường thẳng y = x tại C.
- Tọa độ điểm C:
Hoành độ giao điểm của 2 đồ thị hàm số là nghiệm của phương trình:
x = 2 => y = 2 => tọa độ C(2; 2)
- Tính diện tích tam giác ABC: (với BC là đáy, AE là chiều cao tương ứng với đáy BC)
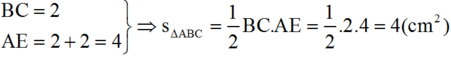
a)
+) y = 2x + 2
Cho x = 0 => y = 2
=> ( 0 ; 2 )
y = 0 => x = -1
=> ( -1 ; 0 )
- Đồ thị hàm số y = x đi qua 2 điểm có tọa độ ( 0 ; 0 )
- Đồ thị hàm số y = 2x + 2 đi qua 2 điểm có tọa độ ( 0 ; 2 ) và ( -1 ; 0 )
b) Hoành độ điểm A là nghiệm của PT sau :
x = 2x + 2
<=> 2x - x = -2
<=> x = -2
=> y = -2
Vậy A ( -2 ; -2 )
c) Tung độ điểm C = 2 => hoành độ điểm C là x = 2
=> C ( 2 ; 2 )
Từ A hạ \(AH\perp BC\), ta có : AH = 4cm
BC = 2cm
Vậy : ..............
\(\Rightarrow S_{ABC}=\frac{1}{2}AH.BC=\frac{1}{2}.4.2=4\left(cm^2\right)\)

a) - Vẽ đồ thị hàm số y = 0,5x + 2 (1)
Cho x = 0 => y = 2 được D(0; 2)
Cho y = 0 => 0 = 0,5.x + 2 => x = -4 được A(-4; 0)
Nối A, D ta được đồ thị của (1).
- Vẽ đồ thị hàm số y = 5 – 2x (2)
Cho x = 0 => y = 5 được E(0; 5)
Cho y = 0 =>0 = 5 – 2x => x = 2,5 được B(2,5; 0)
Nối B, E ta được đồ thị của (2).
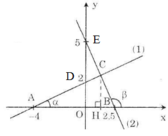
b) Ở câu a) ta tính được tọa độ của hai điểm A và B là A(-4 ; 0) và B (2,5 ; 0)
Hoành độ giao điểm C của hai đồ thị (1) và (2) là nghiệm của phương trình:
0,5 x + 2 = 5 - 2x
⇔ 0,5x + 2x = 5 – 2
⇔ 2,5.x = 3 ⇔ x = 1,2
⇒ y = 0,5.1,2 + 2 = 2, 6
Vậy tọa độ điểm C(1,2; 2,6).
c) AB = AO + OB = |-4| + |2,5| = 6,5 (cm)
Gọi H là hình chiếu của C trên Ox, ta có H( 1,2; 0)
Ta có: AH = AO + OH = 4 + 1,2 = 5,2
BH = BO – OH = 2,5 – 1,2 = 1,3
CH = 2,6
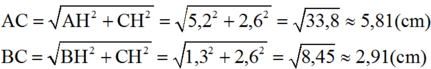
d) Gọi α là góc hợp bởi đường thẳng y = 0,5x + 2 với tia Ox.
Ta có: tgα = 0,5 => α = 26o34'
Gọi β là góc hợp bởi đường thẳng y = 5 - 2x với tia Ox
Tam giác OEB vuông tại O nên:
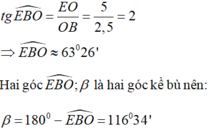
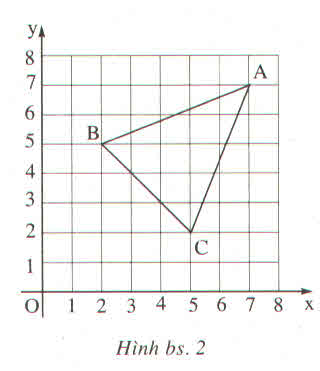


* Áp dụng định lý Py-ta-go vào tam giác vuông lần lượt có các cạnh huyền là AB, AC, BC và sử dụng máy tính bỏ túi, tính được AB ≈ 5,39cm; AC ≈ 5,39; BC ≈ 4,24cm.
Do chu vi của tam giác ABC là AB + BC + CA ≈ 15,02cm
*Diện tích tam giác ABC bằng diện tích hình vuông cạnh dài 5cm trừ đi tổng diện tích ba tam giác vuông xung quanh (có cạnh huyền lần lượt là AB, BC, CA). Tính được: S A B C = 10,5 ( c m 2 ).