Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

∠(P3) và ∠(Q2) là hai góc trong cùng phía.
Trong đó: ∠(P3) = 30º
*) Ta tính:∠(Q2) :
Hai góc ∠(Q2) và ∠(Q1) là hai góc kề bù nên: ∠(Q2) = 180º - ∠(Q1) = 180º – 30º = 150º

a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)

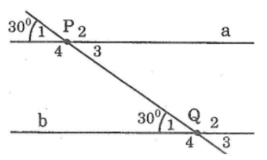
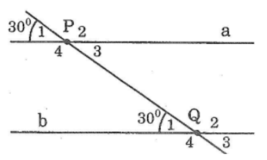
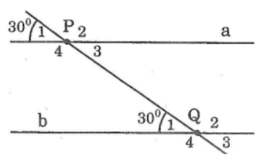
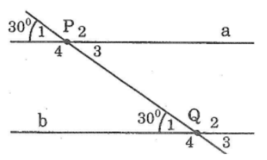
Bài 20 (Sách bài tập - tập 1 - trang 105)
Trên hình 5 người ta cho biết a // b và P1ˆ=Qˆ1=300P1^=Q^1=300

a) Viết tên một cặp góc đồng vị khác và nói rõ số đo mỗi góc
b) Viết tên một cặp góc so le trong và nói rõ số đo của mỗi góc
c) Viết tên một cặp góc trong cùng phía và nói rõ số đo mỗi góc
d) Viết tên một cặp góc ngoài cùng phía và cho biết tổng số đo hai góc đó

∠(P1) và ∠(Q4) là hai góc ngoài cùng phía
∠(P1) = 30º; ∠(Q4) = 150º.
*) Ta tính: ∠(Q4)
Hai góc ∠(Q1) và ∠(Q4) là hai góc kề bù nên: ∠(Q4) = 180º - ∠(Q1) = 180º – 30º = 150º

Cặp góc đồng vị khác là: ∠(P3) = ∠(Q3)
Ta có hai góc ∠(P3) và ∠(P1) là hai góc đối đỉnh nên ∠(P3) = ∠(P1) = 30º
Lại có : hai góc ∠(Q3) và ∠(Q1) là hai góc đối đỉnh nên ∠(Q3) = ∠(Q1) = 30º
Vậy ∠(P3) = ∠(Q3) = 30º