Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Qua C kẻ đường thẳng song song với BD cắt AD ở E. Do BD//CE nên SBDC = SBDE;
Từ đó ta có:
AABCD = SABD + SBDC = SABD + SBDE = SABE.
Qua B kẻ đường thẳng song song với AC, cắt DC ở E. Gọi M là trung điểm của DE, ta có AM là đường thẳng cần dựng. Theo bài 4A, ta chứng minh được SABCD = SADE.
Mà theo cách dựng điểm M ta có SADM = 0.5.SABCD hay đoạn AM chia tứ giác thành 2 phần có diện tích bằng nhau

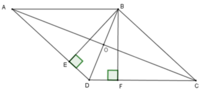
Gọi O là giao điểm của AC, BD.
Vì ABCD là hình thoi nên AC ⊥ BD; OA = OC = A C 2 = 40 cm; OB = OD = B D 2 = 30 cm.
Xét tam giác vuông AOB, theo định lý Pytago ta có:
AB2 = OA2 + OB2 = 402 + 302 = 2500 => 50 CM
Lại có: SABCD = A C . B D 2 = 60.80 2 = 2400 cm2 mà
SABCD = BE. AD ó BE.50 = 2400 ó BE = 48 cm (vì AD = AB = 50 cm)
Xét tam giác vuông BED có: ED2 = BD2 – BE2 = 602 – 482 = 1296 => ED = 36
Suy ra: SBED = 1 2 DE. BE = 1 2 .48.36 = 864 cm2.
Lại có: ΔBED = ΔBFD (ch – gn) nên SBFD = SBED = 864 cm2.
Từ đó: SBEDF = SBFD + SBED = 864 + 864 = 1728 cm2
Đáp án cần chọn là: D
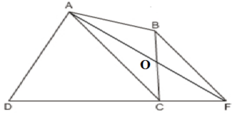
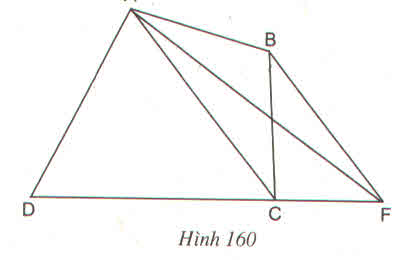

Ta có: BF// AC
⇒ Khoảng cách từ B đến AC bằng khoảng cách từ F đến AC.
⇒ SBAC = SFAC (Chung đáy AC, chiều cao bằng nhau).
⇒ SABC + SADC = SFAC + SADC
hay SABCD = SADF.
Vậy tam giác ADF có diện tích bằng diện tích tứ giác ABCD.