Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a,m_{HCl}=\dfrac{100.7,3}{100}=7,3\left(g\right)\\ \rightarrow n_{HCl}=\dfrac{7,3}{36,5}=0,2\left(mol\right)\\ m_{H_2SO_4}=\dfrac{9,8.100}{100}=9,8\left(mol\right)\\ \rightarrow n_{H_2SO_4}=\dfrac{9,8}{98}=0,1\left(mol\right)\\ n_{CaCO_3}=\dfrac{3}{100}=0,03\left(mol\right)\\ n_{Al}=\dfrac{x}{27}\left(mol\right)\)
PTHH:
\(CaCO_3+2HCl\rightarrow CaCl_2+CO_2\uparrow+H_2O\)
ban đầu 0,03 0,2
phản ứng 0,03 0,06
sau pư 0 0,14 0,03 0,03 0,03
\(2Al+3H_2SO_4\rightarrow Al_2\left(SO_4\right)_3+3H_2\) (*)
- TH1: Al hết \(\dfrac{x}{27}\)------------------------------------->\(\dfrac{x}{18}\)
- TH2: Al dư 0,1------------------------>0,1
\(b,V_{CO_2}=0,03.22,4=0,672\left(l\right)\)
\(c,m_{cốc\left(1\right)}=3+100-0,03.2=102,94\left(g\right)\)
TH1: Al tan hết
\(m_{cốc\left(2\right)}=x+100-\dfrac{x}{18}.2=\dfrac{8x}{9}+100\left(g\right)\)
Do \(m_{cốc\left(1\right)}=m_{cốc\left(2\right)}\)
\(\rightarrow102,94=\dfrac{8x}{9}+100\\ \Leftrightarrow x=3,3075\left(g\right)\)
\(V_{H_2}=\dfrac{3,3075}{18}.22,4=4,116\left(l\right)\)
- TH2: Al dư
\(m_{cốc\left(2\right)}=x+100-0,1.2=99,8+x\left(g\right)\)
\(\rightarrow102,94=99,8+x\\ \Leftrightarrow x=3,14\left(g\right)\)
\(V_{H_2}=0,1.22,4=2,24\left(l\right)\)
\(d,\left\{{}\begin{matrix}C\%_{CaCl_2}=\dfrac{0,03.111}{102,94}.100\%=3,23\%\\C\%_{HCl\left(dư\right)}=\dfrac{0,14.36,5}{102,94}.100\%=4,96\%\end{matrix}\right.\)

- Cốc A: \(CaCO_3+2HCl\rightarrow CaCl_2+CO_2+H_2O\)
\(n_{CaCO_3}=\dfrac{25}{100}=0,25\left(mol\right)=n_{CO_2}\)
Có: m cốc A tăng = mCaCO3 - mCO2 = 25 - 0,25.44 = 14 (g) = m cốc B tăng
- Cốc B: \(2Al+6HCl\rightarrow2AlCl_3+3H_2\)
GọI: nAl = x (mol) \(\Rightarrow n_{H_2}=\dfrac{3}{2}n_{Al}=\dfrac{3}{2}x\left(mol\right)\)
Có: m cốc B tăng = 14 (g) = 27x - 3/2x.2
⇒ x = 7/15 (mol)
\(\Rightarrow a=m_{Al}=\dfrac{7}{15}.27=12,6\left(g\right)\)

Cốc 1: Cho vào cốc(1) 25(g) CaCO3
\(CaCO_3\left(0,25\right)+2HCl\rightarrow CaCl_2+CO_2\left(0,25\right)+H_2O\)
\(n_{CaCO_3}=\dfrac{25}{100}=0,25\left(mol\right)\)
\(\Rightarrow m_{CO_2}=0,25.44=11\left(g\right)\)
Khối lượng của cốc 1 thay đổi là: \(25-11=14\left(g\right)\)
Cốc 2: Cho vào cốc(2) a (g)Al
\(2Al\left(\dfrac{a}{27}\right)+3H_2SO_4\rightarrow Al_2\left(SO_4\right)_3+3H_2\left(\dfrac{a}{18}\right)\)
\(n_{Al}=\dfrac{a}{27}\left(mol\right)\)
\(\Rightarrow m_{H_2}=\dfrac{a}{18}.2=\dfrac{a}{9}\left(g\right)\)
Khối lượng của cốc 2 thay đổi là: \(a-\dfrac{a}{8}=\dfrac{7a}{8}\left(g\right)\)
Vì cân thăng bằng nên ta có
\(\dfrac{7a}{8}=14\Leftrightarrow a=16\left(g\right)\)
Vậy để cân vẫn thăng bằng thì khối lượng Al cần thêm vào là 16(g)

Giả sử ban đầu mcốc A = mcốc B = m (g)
- Xét cốc A:
\(n_{Na}=\dfrac{1,15}{23}=0,05\left(mol\right)\)
PTHH: 2Na + 2HCl --> 2NaCl + H2
0,05-------------------->0,025
=> mcốc A (sau pư) = m + 1,15 - 0,025.2 = m + 1,1 (g)
- Xét cốc B
Gọi số mol Mg thêm vào là a (mol)
PTHH: Mg + 2HCl --> MgCl2 + H2
a---------------------->a
=> mcốc B (sau pư) = m + 24a - 2a = m + 22a (g)
Do mcốc A (sau pư) = mcốc B (sau pư)
=> m + 1,1 = m + 22a
=> a = 0,05 (mol)
=> mMg = 0,05.24 = 1,2 (g)

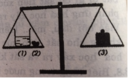
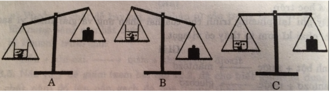
Chọn B. Vì khi cho đá vôi vào dung dịch axit clohiric có phản ứng sinh ra khí cacbon dioxit thoát ra ngoài làm cho khối lượng sẽ giảm đi.
Gọi cốc chứa dung dịch HCl là A
Cốc chứa dung dịch H2SO4 là B
Theo để ta có các PTHH:
CaCO3 + 2HCl \(\xrightarrow[]{}\) CaCl2 + H2O + CO2 (1)
2Al + 3H2SO4 \(\rightarrow\) Al2(SO4)3 + 3H2 (2)
Theo đề: \(n_{CaCO_3}\)= \(\dfrac{25}{100}\)= 0,25 (mol)
Theo PTHH (1): \(n_{CO_2}\) = \(n_{CaCO_3}\) = 0,25 (mol)
=> m\(_{CO_2}\) = 0,25\(\times\)44= 11 (g)
Sau phản ứng ở phương trình (1), khí CO2 bay đi nên sau khi cho thêm 25 gam CaCO3 vào cốc A (vào dung dịch HCl) thì khối lượng cốc A tăng thêm: 25-11=14 (g)
Theo đề: nAl = \(\dfrac{a}{27}\) (mol)
Theo PTHH (2): n\(_{H_2}\)= \(\dfrac{3}{2}\)nAl = \(\dfrac{3}{2}\times\dfrac{a}{27}\)= \(\dfrac{a}{18}\) (mol)
=> m\(_{H_2}\)= \(\dfrac{a}{18}\times2\) = \(\dfrac{a}{9}\) (g)
Sau phản ứng ở phương trình (2), khí H2 bay đi nên sau khi cho thêm a gam Al vào cốc B (vào dung dịch H2SO4) thì khối lượng cốc B tăng thêm: a-\(\dfrac{a}{9}\) (g)
Theo định luật bảo toàn khối lượng thì cốc B cũng phải tăng thêm 14 g
=> a-\(\dfrac{a}{9}\) = 14 (g)
Giải ra ta được: a= 15,75 (g)
Vậy a= 15,75 g