Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Đường thẳng \(d:y = 2x + 3\) có hệ số góc là \(a = 2\).
Đường thẳng \(d':y = 2x - 2\) có hệ số góc là \(a' = 2\).
Hệ số góc của hai đường thẳng \(d\) và \(d'\) bằng nhau.
Từ đồ thị ta thấy, hai đường thẳng \(d\) và \(d'\) song song với nhau.
b) Đường thẳng \(d''\) đi qua gốc tọa độ \(O\) nên có dạng \(y = a''x\).
Từ đồ thị ta thấy, \(d''\) đi qua điểm \(\left( {1;2} \right)\) nên ta có:
\(2 = 1.a'' \Rightarrow a'' = 2\).
Do đó, đường thẳng \(d''\) là \(y = 2x\).

a)
* Xét đường thẳng y = x
Cho x = 1 suy ra y = 1 nên điểm (1; 1) thuộc đường thẳng y = x
Đường thẳng y = x đi qua 2 điểm O(0; 0) và (1; 1)\
* Xét đường thẳng y = -x + 2
Cho x = 2 thì y = -2 + 2 = 0 nên điểm (2; 0) thuộc đường thẳng y = - x+ 2
Cho y = 2 suy ra x = 0 nên điểm (0; 2 ) thuộc đường thẳng y = -x + 2
Đường thẳng y = - x + 2 đi qua hai điểm (2; 0) và (0; 2)
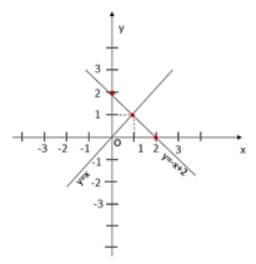
b) Giao điểm A của hai đường thẳng đã cho là A(1;1)
c) Cho y =0 ta được −x + 2 = 0 hay x = 2, suy ra B(2; 0).
Gọi C là giao điểm của đường thẳng y = −x + 2 và trục Oy. Suy ra C(0; 2). Dễ thấy tam giác OBC vuông cân tại O (vì OB = OC = 2).
Xét hai tam giác OAB và OAC có:
cạnh OA chung;
OB = OC;
\( \widehat {OBA} = \widehat {OCA} = 45^0\)
Do đó \(\Delta OAB = \Delta OAC\), từ đó suy ra AB = AC.
Điều này chứng tỏ A là trung điểm của BC, mà \(\Delta OBC \) cân tại O nên \(OA \bot AB\), tức là \(\Delta OAB\) vuông tại A.
d)
Đường thẳng y = x có hệ số góc bằng 1.
Đường thẳng y = - x + 1 có hệ số góc bằng -1
Tích của hai hệ số góc bằng -1

Xét (d): y = 2x+1:
Cho y = 0 thì \(x = \frac{{ - 1}}{2}\), ta được giao điểm của đồ thị với trục Ox là A(\(\frac{{ - 1}}{2};0\))
x = 0 thì y = 1, ta được giao điểm của đồ thị với trục Oy là B(0;1)
Xét (d'): y = −2x+1:
Cho y = 0 thì \(x = \frac{1}{2}\), ta được giao điểm của đồ thị với trục Ox là \(C\left( {\frac{1}{2};0} \right)\)
x = 0 thì y = 1, ta được giao điểm của đồ thị với trục Oy là B(0;1)


a) Vẽ đường thẳng y = 2x -1 trên mặt phẳng tọa độ
Với x = 0 thì y = -1, ta được điểm A(0; -1) thuộc đồ thị hàm số y = 2x – 1
Với x = 1 thì y = 1, ta được điểm B(1; 1) thuộc đường thẳng y = 2x – 1
Đồ thị hàm số y = 2x – 1 là một đường thẳng đi qua hai điểm A(0; -1) và điểm B(1; 1)
b) Vì đường thẳng y = ax + b \(\left( {a \ne 0} \right)\) song song với đường thẳng y = 2x -1 nên a = 2
Đường thẳng dã cho là: y = 2x + b
Vì đường thẳng y = 2x + b đi qua điểm M(1; 3) nên:
3 = 2.1 + b suy ra b = 1
Vậy đường thẳng cần tìm là; y = 2x + 1
* Vẽ đường thẳng y = 2x + 1
Với x = 0 thì y = 1, ta được điểm P(0, 1) thuộc đồ thị hàm số y = 2x + 1
Với x = 1 thì y = 1, ta được điểm Q(1; 3) thuộc đồ thị hàm số y = 2x + 1
Đồ thị hàm số y = 2x + 1 là đường thẳng đi qua hai điểm P(0; 1) và Q(1; 3)

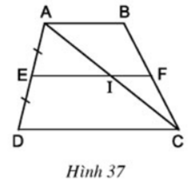
Áp dụng định lí 1 đường trung bình của tam giác
ΔADC có E là trung điểm AD và EI song song với cạnh DC
⇒ Điểm I là trung điểm AC
ΔABC có I là trung điểm AC và FI song song với cạnh AB
⇒ điểm F là trung điểm BC

a)
- Vẽ đồ thị hàm số \(y = x\).
Cho \(x = 1 \Rightarrow y = 1 \Rightarrow \)Đồ thị hàm số đi qua điểm \(M\left( {1;1} \right)\).
Đồ thị hàm số \(y = x\) là đường thẳng đi qua hai điểm \(O\) và \(M\).
- Vẽ đồ thị hàm số \(y = x + 2\)
Cho \(x = 0 \Rightarrow y = 2\) ta được điểm \(A\left( {0;2} \right)\) trên trục \(Oy\).
Cho \(y = 0 \Rightarrow x = \dfrac{{ - 2}}{1} = - 2\) ta được điểm \(B\left( { - 2;0} \right)\) trên \(Ox\).
Đồ thị hàm số \(y = x + 2\) là đường thẳng đi qua hai điểm \(A\) và \(B\).
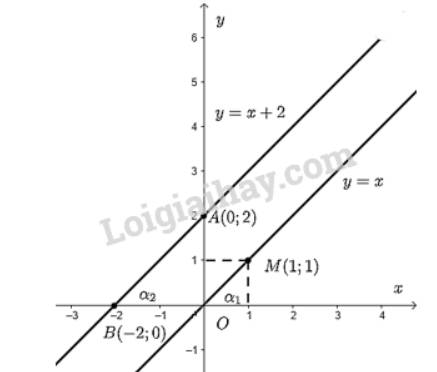
b) Góc tạo bởi hai đường thẳng \(y = x\) và \(y = x + 2\) với trục \(Ox\) lần lượt là \({\alpha _1}\) và \({\alpha _2}\).
Dùng thước đo độ kiểm tra ta thấy số đo \({\alpha _1} = {\alpha _2} = 45^\circ \).

Áp dụng định lí 1 đường trung bình của tam giác
ΔADC có E là trung điểm AD và EI song song với cạnh DC
⇒ Điểm I là trung điểm AC
ΔABC có I là trung điểm AC và FI song song với cạnh AB
⇒ điểm F là trung điểm BC

a:
Vẽ đồ thị y=2-x
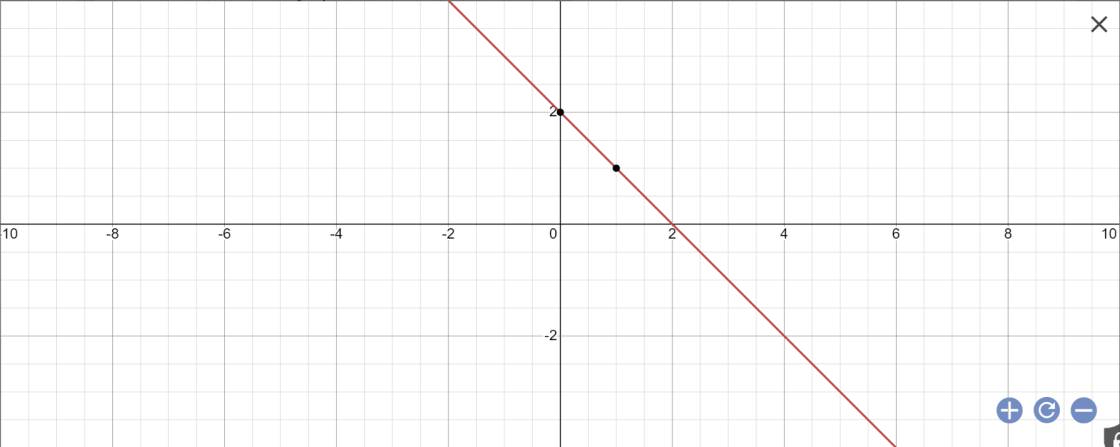
y=2-x
=>y+x-2=0
=>x+y-2=0
Khoảng cách từ O đến đường thẳng x+y-2=0 là:
\(d\left(O;x+y-2=0\right)=\dfrac{\left|0\cdot1+0\cdot1-2\right|}{\sqrt{1^2+1^2}}\)
\(=\dfrac{2}{\sqrt{1+1}}=\dfrac{2}{\sqrt{2}}=\sqrt{2}\)
b:
Vẽ đồ thị y=2x+1
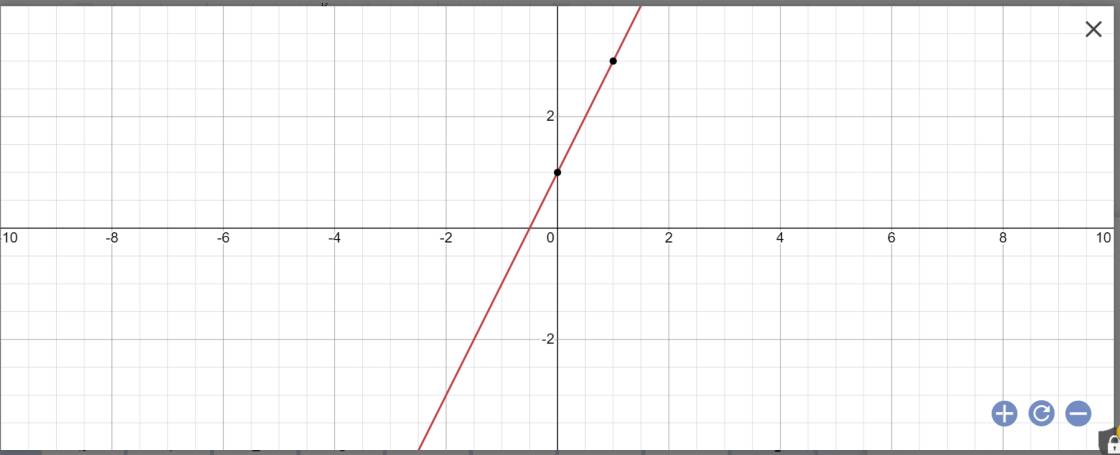
y=2x+1
=>2x-y+1=0
Khoảng cách từ O(0;0) đến đường thẳng y=2x+1 là:
\(\dfrac{\left|0\cdot2+0\cdot\left(-1\right)+1\right|}{\sqrt{2^2+\left(-1\right)^2}}=\dfrac{1}{\sqrt{4+1}}=\dfrac{\sqrt{5}}{5}\)
c:
Vẽ đồ thị \(y=\dfrac{x-2}{2}\)
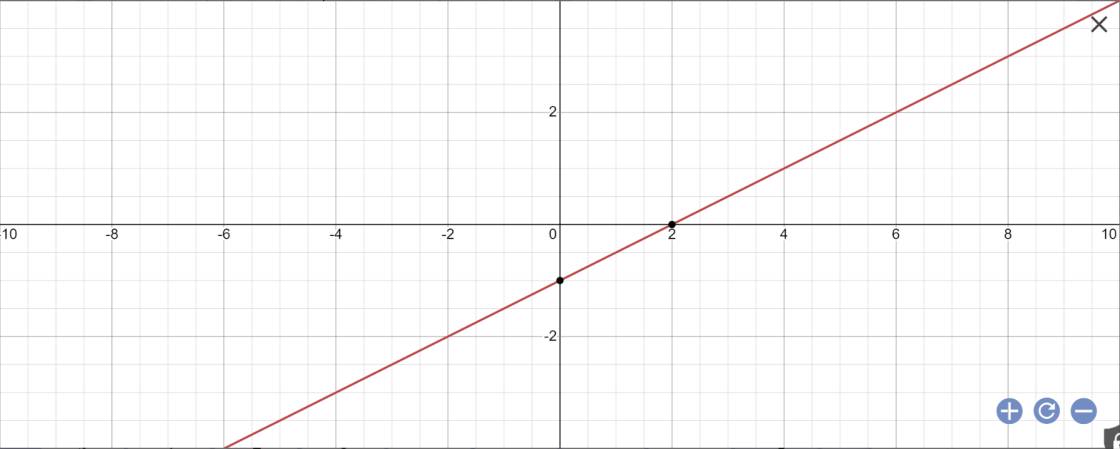
\(y=\dfrac{x-2}{2}\)
=>x-2=2y
=>x-2y-2=0
Khoảng cách từ O(0;0) đến đường thẳng \(y=\dfrac{x-2}{2}\) là:
\(\dfrac{\left|0\cdot1+0\cdot\left(-2\right)-2\right|}{\sqrt{1^2+\left(-2\right)^2}}=\dfrac{\left|-2\right|}{\sqrt{1+4}}=\dfrac{2}{\sqrt{5}}\)
d:
Vẽ đồ thị y=-2x
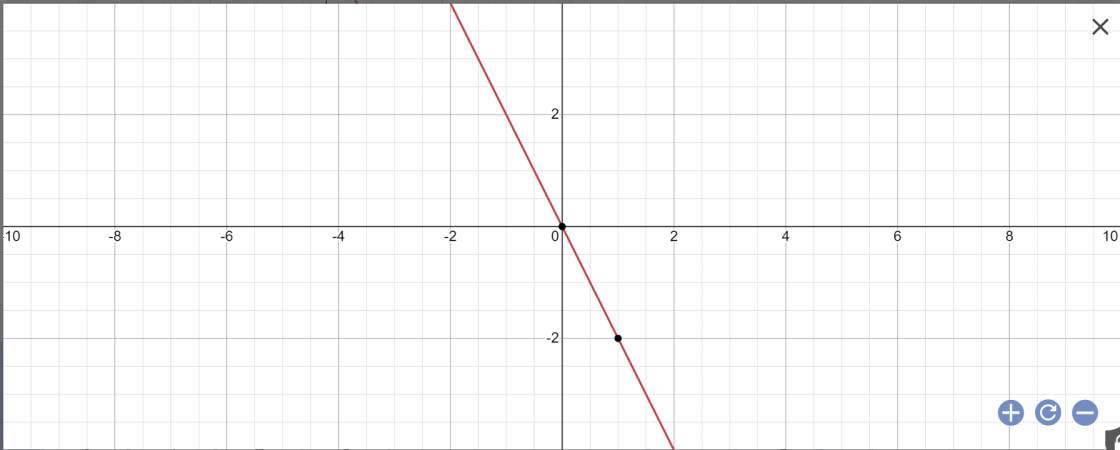
y=-2x
=>-2x+y=0
Khoảng cách từ O(0;0) đến đường thẳng y=-2x là:
\(\dfrac{\left|0\cdot\left(-2\right)+0\cdot1+0\right|}{\sqrt{\left(-2\right)^2+1^2}}=\dfrac{0}{\sqrt{\left(-2\right)^2+1^2}}=0\)
* Xét đường thẳng y = 2x
Cho x = 0 suy ra y = 2.0 = 0 nên điểm (0; 0) thuộc đường thẳng y = 2x
Cho x = 1 suy ra y = 2 nên điểm (1; 2) thuộc đường thẳng y = 2x
Đường thẳng y=2x đi qua 2 điểm (0;0) và (1;2)
* Xét đường thẳng y = 2x + 1
Cho x = 0 suy ra y = 2.0 + 1= 1 nên điểm (0; 1) thuộc đường thẳng y = 2x + 1
Cho \(x = \frac{{ - 1}}{2}\) suy ra \(y = 2.\left( {\frac{{ - 1}}{2}} \right) + 1 = 0\) nên điểm \(\left( {\frac{{ - 1}}{2};0} \right)\) thuộc đường thẳng y = 2x + 1
Đường thẳng y = 2x+1 đi qua 2 điểm (−12;0) và (0;1)