Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Thử:
Gọi 2/5 stn=1/6 sth = x
=> stn=5x/2 ; sth=6x
stn+sth=17x/2=51
x=51:17x2=6
Vậy stn=5x/2=15 ; sth=6x=36
Gọi st1 là x
Số t2 la : 51-x
Theo đề bài ta có pt: \(\frac{2}{5}x=\frac{1}{6}\left(51-x\right)\)
\(\Leftrightarrow\) \(\frac{2}{5}x=\frac{17}{2}-\frac{1}{6}x\)
\(\Leftrightarrow\) \(\frac{2}{5}x+\frac{1}{6}x=\frac{17}{2}\)
\(\Leftrightarrow\) \(\frac{17}{30}x=\frac{17}{2}\)
\(\Leftrightarrow\) \(x=15\)
Vậy :...................................

-Gọi số thứ nhất là x (x∈N*)
-Số thứ hai là: \(26-x\)
-Vì hai lần số thứ nhất hơn ba lần số thứ hai 7 đơn vị nên ta có phương trình:
\(2x-3\left(26-x\right)=7\)
\(\Leftrightarrow2x-78+3x=7\)
\(\Leftrightarrow5x=85\)
\(\Leftrightarrow x=17\left(nhận\right)\)
-Vậy số thứ nhất là 17, số thứ hai là 26-17=9.

Gọi a (a ∈ N *) là số thứ nhất. Ta có số thứ hai là 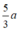
Thương phép chia số thứ nhất cho 9 là a/9
Thương phép chia số thứ hai cho 6 là: 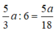
Thương thứ nhất bé hơn thương thứ hai là ba đơn vị nên ta có phương trình:
5a/18 - a/9 = 3
⇔ 5a/18 - 2a/18 = 54/18
⇔ 5a – 2a = 54
⇔ 3a = 54 ⇔ a = 18 (thỏa mãn)
Vậy số thứ nhất là 18, số thứ hai là 5/3.18 = 30.

Bài 1:
Gọi 2 số là a,b (\(a,b\inℤ\))
Ta có: a+b=51(*)
Mà 2/5a=1/6b
=> a=5/12b
Thay vào (*) ta có: 17/12b=51
=>b=36
Bài 1 :
Gọi số thứ nhất và số thứ hai lần lượt là x và y (x,y thuộc z)
Tổng hai số bằng : \(x+y=51\left(1\right)\)
Biết 2/5 số thứ nhất thì bằng 1/6 số thứ hai
\(x\frac{2}{5}-y\frac{1}{6}=0\left(2\right)\)
Từ 1 và 2 ta suy ra được hệ phương trình sau :
\(\hept{\begin{cases}x+y=51\\x\frac{2}{5}-y\frac{1}{6}=0\end{cases}}\)\(< =>\hept{\begin{cases}x=51-y\\\frac{2x}{5}-\frac{y}{6}=0\end{cases}}\)
\(< =>\frac{\left(51-y\right)2}{5}-\frac{y}{6}=0\)\(< =>\frac{102-2y}{5}-\frac{y}{6}=0\)
\(< =>\frac{102-2y}{5}=\frac{y}{6}\)\(< =>\left(102-2y\right)6=5y\)
\(< =>612-12y=5y\)\(< =>612=17y\)
\(< =>y=\frac{612}{17}=36\left(3\right)\)
Thay 3 vào 1 ta được : \(x+y=51\)
\(< =>x+36=51< =>x=51-36=15\)
Vậy số thứ nhất và số thứ hai lần lượt là 15 và 36

Gọi x là kết quả do lấy số thứ 1 cộng 5 thì số thứ 1 là x - 5
Số thứ 2 là x + 5
Số thứ 3 là \(\frac{x}{5}\)
Số thứ 4 là 5x
Ta có: \(\left(x-5\right)+\left(x+5\right)+\frac{x}{5}+5x=720\)
\(\Leftrightarrow7x+\frac{x}{5}=720\Leftrightarrow\frac{36x}{5}=720\Leftrightarrow x=100\)
Vậy số thứ 1 là: x - 5 = 100 - 5 = 95
Số thứ 2 là: 100 + 5 = 105
Số thứ 3 là: \(\frac{100}{5}=20\)
Số thứ 4 là: \(100.5=500\)
Gọi x là kết quả do lấy số thứ 1 cộng 5 thì số thứ 1 là x - 5
Số thứ 2 là x + 5
Số thứ 3 là \frac{x}{5}5x
Số thứ 4 là 5x
Ta có: \left(x-5\right)+\left(x+5\right)+\frac{x}{5}+5x=720(x−5)+(x+5)+5x+5x=720
\Leftrightarrow7x+\frac{x}{5}=720\Leftrightarrow\frac{36x}{5}=720\Leftrightarrow x=100⇔7x+5x=720⇔536x=720⇔x=100
Vậy số thứ 1 là: x - 5 = 100 - 5 = 95
Số thứ 2 là: 100 + 5 = 105
Số thứ 3 là: \frac{100}{5}=205100=20
Số thứ 4 là: 100.5=500100.5=500

+) Gọi số thứ nhất (ban đầu) là x. (x: nguyên, dương)
Khi đó số thứ hai (ban đầu) là \(\dfrac{3}{5}x\)
+) Số thứ nhất sau khi chia cho 9 gọi là \(\dfrac{x}{9}\)
Số thứ hai sau khi chia cho 6 gọi là \(\dfrac{\dfrac{3}{5}x}{6}\)
Vì: thương số thứ nhất chia cho 9 bé hơn thương số thứ hai chia cho 6 là 3 đơn vị nên ta có phương trình:
\(\dfrac{x}{9}+3=\dfrac{\dfrac{3}{5}x}{6}\\ < =>\dfrac{2x}{18}+\dfrac{54}{18}=\dfrac{\dfrac{9}{5}x}{18}\\ < =>2x+54=\dfrac{9}{5}x\\ < =>2x-\dfrac{9}{5}x=-54\\< =>\dfrac{1}{5}x=-54\\ =>x=\dfrac{-54}{\dfrac{1}{5}}=-270\left(loại\right)\)
Vậy: Không thỏa mãn yêu cầu đề bài.

gọi số thứ nhất là a, số thứ hai là b (a,b thuộc Z và khác 0)
Theo đề bài ta có phương trình: a+b=100 và 2a=5(b+5) => a=(5b+25)/2
Thay vào phương trình thứ nhất tìm được b=25
=> a=75
Gọi số thứ nhất là x (x < 51)
Số thứ hai là 51 – x
Theo điều kiện đề bài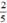 số thứ nhất bằng
số thứ nhất bằng 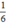 số thứ hai nên ta có phương trình:
số thứ hai nên ta có phương trình: