Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

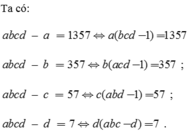
Nếu 1 trong a,b,c,d chẵn thì 1 trong 4 đẳng thức sai (kết quả ra chẵn do 1 số chẵn nhân 1 tích thì chẵn) =>a,b,c,d không tồn tại (do a,b,c,d phải thoả cả 4 đẳng thức)
Nếu a,b,c,d đều lẻ thì 1số lẻ nhân cho 1 số chẵn (tích 3 số lẻ trừ 1 thì chẵn) thì là một số chẵn=>a,b,c,d không tồn tại
Vậy không tồn tại các số nguyên a,b,c,d để thoả yêu cầu đề bài

Đáp án:
Giải thích các bước giải:
Không tồn tại số a,b,c,d
Vì ta có abcd là số có 4 chữ số
abcd-d=7
Số có 4 chữ số - số đơn vị=7( vô lí)
=> không tồn tại a,b,c,d
học tốt

Lời giải:
Giả sử tồn tại các số nguyên a,b,c,d thỏa bài toán
Ta có abcd − a = a(bcd − 1) = 1357 là số lẻ nên a là số lẻ
Tương tự b,c,d cũng là số lẻ
Như vậy abcd lẻ và a lẻ suy ra abcd − a là số chẵn (vô lý)
Vậy không tồn tại các số nguyên a, b, c, d thỏa bài toán
