Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

rút gọn được, nhưng chỉ khi dùng để viết pt đường thẳng thôi

a: VTCP là (3;-5)
=>VTPT là (5;3)
b: 3t-2=14
=>3t=16
=>t=16/3
=>y=-7-5t=-7-80/3=-101/3
c: -5t-7=-12
=>5t+7=12
=>t=1
=>x=-2+3=1
d: H(14;-101/3); G(1;-12)
Tọa đọ trung điểm là:
\(\left\{{}\begin{matrix}x=\dfrac{14+1}{2}=\dfrac{15}{2}\\y=\dfrac{1}{2}\left(-\dfrac{101}{3}-12\right)=-\dfrac{137}{6}\end{matrix}\right.\)

Xét đường thẳng \(\Delta :x + 2y - 5 = 0\)
Vecto \(\overrightarrow n = (1;2)\) là một VTPT của \(\Delta \) => A đúng => Loại A
Vecto \(\overrightarrow u = ( - 2;1)\) là một VTCP của \(\Delta \) => B đúng => Loại B
Đường thẳng \(\Delta \)có hệ số góc \(k = - \frac{a}{b} = - \frac{1}{2}\) => D sai => Chọn D
Chọn D.

\(\left\{{}\begin{matrix}\overrightarrow{AB}=\left(1;-1\right)\\\overrightarrow{BC}=\left(-3;4\right)\end{matrix}\right.\)
\(\Rightarrow\overrightarrow{u}=3\overrightarrow{AB}+2\overrightarrow{BC}=\left(-3;5\right)\)
Gọi \(D\left(x;y\right)\Rightarrow\overrightarrow{DC}=\left(1-x;5-y\right)\)
Để ABCD là hbh \(\Leftrightarrow\overrightarrow{AB}=\overrightarrow{DC}\)
\(\Leftrightarrow\left\{{}\begin{matrix}1-x=1\\5-y=-1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=0\\y=6\end{matrix}\right.\)
\(\Rightarrow D\left(0;6\right)\)

\(\overrightarrow{c}=2\left(2;1\right)+3\left(3;-2\right)=\left(4+9;2-6\right)=\left(13;-4\right)\)

Bài 1:
Ta có:
\(\overrightarrow{AB}-\overrightarrow{CB}+\overrightarrow{CD}-\overrightarrow{ED}\)
\(=(\overrightarrow{AC}+\overrightarrow{CB})-\overrightarrow{CB}+(\overrightarrow{CE}+\overrightarrow{ED})-\overrightarrow{ED}\)
\(=\overrightarrow{AC}+\overrightarrow{CE}=\overrightarrow{AE}\)
Bài 2: Đề bài không rõ ràng, bạn xem lại hộ mình nhé.
bạn ơi câu 2 mình ghi sai đề bạn mình ghi lại bạn giúp mình với
2) trong mặt phảng OXY, cho tam giác ABC có A(-3;5) B(1;-1) C(2;4)
a) Tìm vtAB và trọng tâm G của tam giác ABC
b) Tìm tọa độ D sao cho vtCD=2vtAB
c) Tính vtCA* vtBC
d) Tính chu vi và diện tích tam giác ABC
e) tính góc B của tam giác ABC
f) Tìm tọa độ điểm E thuộc oX sao cho | VTEA+ vtEB+vtEC|

a) Đúng.
Hai vec tơ đối nhau thì chúng có hoành độ đối nhau và tung độ đối nhau.
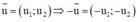
b) Sai.
Sửa lại: Vec tơ a→ cùng phương với vec tơ i→ nếu a→ có tung độ bằng 0.
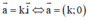
c) Đúng.
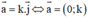
Có thể hiểu nôm na là khi tính vecto pháp tuyến, chỉ phương hoặc cần tỉ lệ để tính song song thì có thể "rút gọn", còn khi tính độ dài, tính góc thì không được (tính toán liên quan độ dài thì tuyệt đối ko được "rút gọn" vecto, còn tính toán góc thì chỉ rút gọn khi thực sự hiểu).