PT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
CM
13 tháng 8 2018
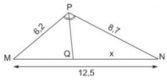
Ta có: MQ + QN = MN nên MQ = MN - QN = 12,5 - x
ΔPMN có PQ là phân giác
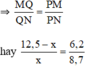
⇔ 8,7.(12,5 – x) = x.6,2
⇔ 108,75 – 8,7.x = 6,2.x
⇔ 108,75 = 14,9x hay 14,9.x = 108,75
⇔ x ≈ 7,3.
SG
4
TQ
29 tháng 1 2018
a)Vì AD là phân giác của góc BAC
=>\(\dfrac{DC}{BD}=\dfrac{AC}{AB}\) <=>\(\dfrac{x}{3.5}=\dfrac{7.2}{4.5}\) <=>x=\(\dfrac{7.2X3.5}{4.5}\) <=>x=5.6
b)vì PQ là phân giác của góc MPN
=>\(\dfrac{QN}{MQ}=\dfrac{PN}{PM}\) <=>
22 tháng 4 2017
a) AD là tia phân giác của ∆ABC nên
= => DC = =
=> x = 5,6
b) PQ là đường phân giác của ∆PMN nên =
Hay =
Áp dụng tính chất của tỉ lệ thức:
=> = = =
=> x≈ 7,3
2 tháng 3 2022
1.Làm tròn số 92,117 đến hàng phần mười được kết quả là:92,1
2.Làm tròn số -845,654 đến hàng phần mười (đến chữ số thập phân thứ nhất) được kết quả là:-845,7
3.Làm tròn số 82,572 đến hàng phần mười được kết quả là:82,6
4.Làm tròn số 82,572 đến hàng phần mười được kết quả là:82,6
5.Làm tròn số -72,882 đến chữ số thập phân thứ nhất được kết quả là:-72,9
CM
13 tháng 5 2018
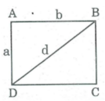
Giả sử hình chữ nhật ABCD có AB = b = 5cm; AD= a = 3cm; BD = d.
Áp dụng định lí Pi-ta-go vào tam giác vuông ABD, ta có:
d 2 = a 2 + b 2
⇒ d 2 = 3 2 + 5 2 = 9 + 25 = 34
Vậy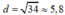 
(cm).
HT
1
30 tháng 6 2017
Theo định lý Py-ta-go :
\(d^2=a^2+b^2=3^2+5^2=34\)
hay \(d=\sqrt{34}\approx5,8\left(cm\right)\)
16 tháng 10 2017
Giả sử hình chữ nhật ABCD có AB = a = 3cm; BC = b = 5cm; BD = d
Trong tam giác vuông ABC theo định lý Py-ta-go ta có:
d2=a2+b2⇒d2=32+52=9+25=34d=√34≈5,8(cm)
CM
15 tháng 5 2019
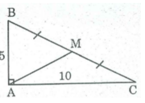
Giả sử tam giác ABC có ∠ A = 90 0 , M trung điểm BC; AB = 5cm, AC = 10cm
Áp dụng định lý Pi-ta-go vào tam giác vuông ABC, ta có:
B C 2 = A B 2 + A C 2
BC = 5 2 + 10 2 = 125 ≈ 11,2 (cm)
Mà AM = 1/2 BC (tính chất tam giác vuông)
⇒ AM = 1/2 .11,2 = 5,6 (cm)
CM
26 tháng 4 2018
Điều kiện xác định: x ≠ 0 và x ≠ 5.
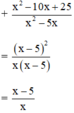
Tại x = 1,12, giá trị phân thức bằng: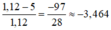 
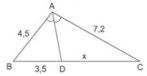
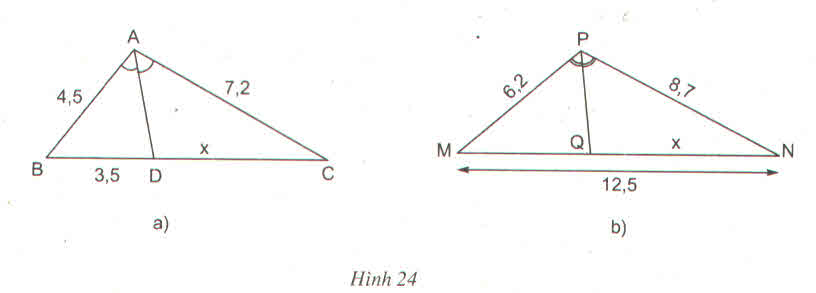
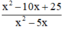
ΔABC có AD là đường phân giác