Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
T=(1-1/2).(1-1/3).(1-1/4)....(1-1/10)
T=1/2.2/3.3/4.4/5....9/10
T=1.9/10
T=9/10
BÀI TOÁN DỄ NHẤT ĐẤY
\(T=\left(1-\dfrac{1}{3}\right)\left(1-\dfrac{1}{5}\right)\left(1-\dfrac{1}{7}\right)\left(1-\dfrac{1}{9}\right)\left(1-\dfrac{1}{2}\right)\left(1-\dfrac{1}{4}\right)\left(1-\dfrac{1}{6}\right)\left(1-\dfrac{1}{8}\right)\left(1-\dfrac{1}{10}\right)\)\(\Rightarrow T=\dfrac{2}{3}.\dfrac{4}{5}.\dfrac{6}{7}.\dfrac{8}{9}.\dfrac{10}{11}.\dfrac{1}{2}.\dfrac{3}{4}.\dfrac{5}{6}.\dfrac{7}{8}.\dfrac{9}{10}\)
\(\Rightarrow=\dfrac{1}{11}\)
\(\Rightarrow\) Số nghịch đảo của T là \(11\)
\(T=\left(1-\frac{1}{3}\right)\left(1-\frac{1}{5}\right)\left(1-\frac{1}{7}\right)\left(1-\frac{1}{9}\right)\left(1-\frac{1}{11}\right)\left(1-\frac{1}{2}\right)\left(1-\frac{1}{4}\right)\left(1-\frac{1}{6}\right)\left(1-\frac{1}{8}\right)\left(1-\frac{1}{10}\right)\)
\(T=\frac{2}{3}.\frac{4}{5}.\frac{6}{7}.\frac{8}{9}.\frac{10}{11}.\frac{1}{2}.\frac{3}{4}.\frac{5}{6}.\frac{7}{8}.\frac{9}{10}=\frac{\left(2.4.6.8.10\right).\left(1.3.5.7.9\right)}{\left(3.5.7.9.11\right).\left(2.4.6.8.10\right)}=\frac{1}{11}\)
Đáp số: T=1/11
T=( 1-1/3) (1-1/5) (1-1/7) ( 1- 1/9) (1-1/11) (1-1/2) ( 1-1/4) ( 1-1/6) (1-1/8) (1-1/10)
\(=\left(1-\frac{1}{2}\right)\left(1-\frac{1}{3}\right)\left(1-\frac{1}{4}\right)...\left(1-\frac{1}{11}\right)\)
\(=\frac{1}{2}\cdot\frac{2}{3}\cdot\frac{3}{4}\cdot...\cdot\frac{10}{11}\)
\(=\frac{1\cdot2\cdot3\cdot...\cdot10}{2\cdot3\cdot4\cdot...\cdot11}\)
\(=\frac{1}{11}\)
Ta có
\(A=\left(1-\frac{1}{3}\right)\left(1-\frac{1}{5}\right).....\left(1-\frac{1}{11}\right)\left(1-\frac{1}{2}\right)\left(1-\frac{1}{4}\right)......\left(1-\frac{1}{10}\right)\)
\(\Leftrightarrow A=\left(1-\frac{1}{2}\right)\left(1-\frac{1}{3}\right)\left(1-\frac{1}{4}\right).....\left(1-\frac{1}{11}\right)\)
\(\Leftrightarrow A=\frac{1.2.3.....10}{2.3.4.....11}=\frac{1}{11}\)
\(1.\)\(M=\frac{1}{2}+\frac{1}{6}+\frac{1}{12}+...+\frac{1}{42}\)
\(M=\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{6.7}\)
\(M=\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-...+\frac{1}{6}-\frac{1}{7}\)
\(M=1-\frac{1}{7}=\frac{6}{7}\)
Mình làm câu 1 thoi nha!
1.
\(\frac{1}{2}+\frac{1}{6}+\frac{1}{12}+\frac{1}{20}+\frac{1}{30}+\frac{1}{42}\)
=\(\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+\frac{1}{4.5}+\frac{1}{5.6}+\frac{1}{6.7}\)
=\(\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{6}-\frac{1}{7}\)
=\(1-\frac{1}{7}\)
=\(\frac{6}{7}\)
Ta có: \(P=\left(1-\dfrac{1}{2}\right)\left(1-\dfrac{1}{3}\right)\cdot...\cdot\left(1-\dfrac{1}{11}\right)\)
\(=\dfrac{-1}{2}\cdot\dfrac{-2}{3}\cdot...\cdot\dfrac{-9}{10}\cdot\dfrac{-10}{11}\)
\(=\dfrac{1}{2}\cdot\dfrac{2}{3}\cdot...\cdot\dfrac{9}{10}\cdot\dfrac{10}{11}\)
\(=\dfrac{1}{11}\)
\(\dfrac{2}{3}.\dfrac{4}{5}.\dfrac{6}{7}.\dfrac{8}{9}.\dfrac{10}{11}.\dfrac{1}{2}.\dfrac{3}{4}.\dfrac{5}{6}.\dfrac{7}{8}.\dfrac{9}{10}\)
= \(\dfrac{1}{2}.\dfrac{2}{3}.\dfrac{3}{4}.\dfrac{4}{5}.\dfrac{5}{6}.\dfrac{6}{7}.\dfrac{7}{8}.\dfrac{8}{9}.\dfrac{9}{10}.\dfrac{10}{11}\)
= \(\dfrac{1}{11}\)
Số nghịch đảo của \(\dfrac{1}{11}\)là \(\dfrac{11}{1}=11\)
\(a=\dfrac{1}{3}-\dfrac{1}{4}=\dfrac{4-3}{12}=\dfrac{1}{12}\)
\(\rightarrow\) Số nghịch đảo của \(a\) là \(12.\)
\(b=\dfrac{2}{7}.\dfrac{14}{5}-1=\dfrac{4}{5}-1=-\dfrac{1}{5}\)
\(\rightarrow\) Số nghịch đảo của \(b\) là \(-5.\)
\(c=\dfrac{3}{4}-\dfrac{1}{25}.5=\dfrac{3}{4}-\dfrac{1}{5}=\dfrac{15-4}{20}=\dfrac{11}{20}\)
\(\rightarrow\) Số nghịch đảo của \(c\) là \(\dfrac{20}{11}.\)
\(d=-8.\left(6.\dfrac{1}{24}\right)=-8.\dfrac{1}{4}=-2\)
\(\rightarrow\) Số nghịch đảo của \(d\) là \(\dfrac{1}{-2}\) hay \(-\dfrac{1}{2}.\)
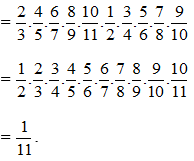
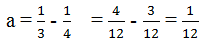. số nghịch đảo của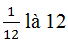 
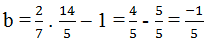. số nghịch đảo của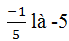 
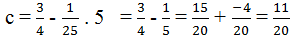. số nghịch đảo của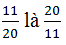 
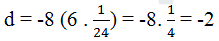. số nghịch đảo của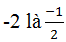 
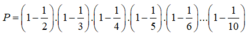
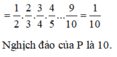
Số nghịch đảo của 1/11 là 11