Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Lâu ko ôn lại cũng hơi miss tích phân r :v
\(\int\limits^{\dfrac{-\pi}{4}}_{\dfrac{\pi}{4}}\tan x.dx\)
\(\int\tan x.dx=\int\dfrac{\sin x}{\cos x}.dx=-\int\dfrac{1}{\cos x}.d\left(\cos x\right)=-ln\left|\cos x\right|\)
\(\Rightarrow\int\limits^{\dfrac{-\pi}{4}}_{\dfrac{\pi}{4}}\tan x.dx=-ln\left|\cos\dfrac{-\pi}{4}\right|+ln\left|\cos\dfrac{\pi}{4}\right|\)
\(\int_{\frac{\pi}{6}}^{\frac{\pi}{3}}\frac{1}{sin^4x.cosx}d\pi x\)
Tập xác định D= R\{1}.
Đạo hàm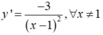 
(C) có tiệm cận đứng x=1 (d1) và tiệm cận ngang y=2 (d2) nên I(1 ;2).
Gọi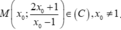 
.
Tiếp tuyến ∆ của (C) tại M có phương trình
∆ cắt d1 tại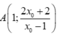 
và cắt d2 tại 
.
Ta có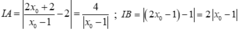 
.
Do đó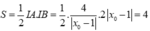 
.
Chọn C.
Tập xác định D= R\ { 1}.
Đạo hàm y ' = - 3 ( x - 1 ) 2 , ∀ x ≠ 1 .
Đồ thị hàm số C có tiệm cận đứng là x= 1 và tiệm cận ngang y= 2 nên I (1 ;2 ) là giao của 2 đường tiệm cận.
Gọi M ( x 0 ; 2 x 0 + 1 x 0 - 1 ) ∈ ( C ) , x 0 ≠ 1 .
Tiếp tuyến ∆ của C tại M có phương trình là :
⇔ y = - 3 ( x 0 - 1 ) 2 ( x - x 0 ) + 2 x 0 + 1 x 0 - 1
∆ cắt TCĐ tại A ( 1 ; 2 x 0 + 2 x 0 - 1 ) và cắt TCN tại B( 2x0-1 ; 2) .
Ta có I A = 2 x 0 + 2 x 0 - 1 - 2 = 4 x 0 - 1 ; I B = ( 2 x 0 - 1 ) - 1 = 2 x 0 - 1 .
Do đó, S = 1 2 I A . I B = 1 2 4 x 0 - 1 . 2 x 0 - 1 = 4 .
Chọn D.
= -2³/3 + 2²/2 + 2.2 - [-(-1)³/3 + (-1)²/2 + 2.(-1)]
= -8/3 + 2 + 4 - 1/3 - 1/2 + 2
= 8 - 3 - 1/2
= 9/2
\(\int\limits^2_{-1}\left(-x^2+x+2\right)dx=\left(-\dfrac{x^3}{3}+\dfrac{x^2}{2}+2x\right)|^2_{-1}=\dfrac{9}{2}\)
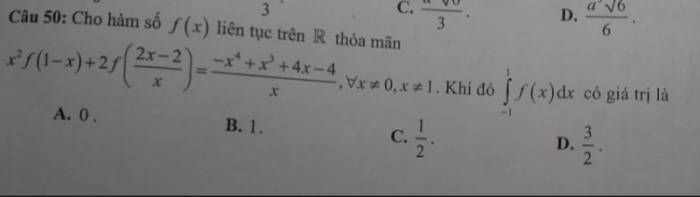mọi người cho mình hỏi làm sao để xác định được cận của tích phân chạy từ 1 đến 2 ở bài này ? 
Nhân phân phối sinx vào, tách ra 2 tích phân
Tích phân đầu nguyên hàm sinx là ra
Tích phân 2, đặt t=sinx => dt=cosxdx, đổi cận, thế vào, nguyên hàm lại là ra