Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Gọi O là hình chiếu của S lên A B C ; S O = S B 2 − B O 2 = 4 a 2 − a 2 3 = a 33 3
V = 1 3 S Δ A B I . S O = 1 3 . a 2 3 8 . a 33 3 = a 3 11 24

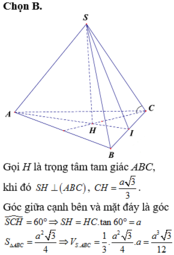
Chọn B.
Phương pháp: Mấu chốt bài toán là chỉ ra được tam giác SAC vuông tại S.
Cách giải: Gọi O là giao điểm của AC và BD, H là hình chiếu của S lên mặt đáy.



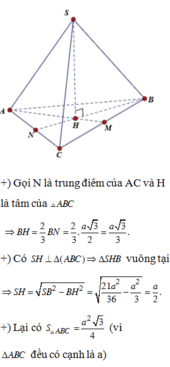
Đáp án D
Ta có:
S A B C = A B 2 3 4 = 3 2 ⇒ V S . A B C = 1 3 . S A . S A B C = 1 2 .

Đáp án C

Gọi H là trực tâm của tam giác đều ABC ⇒ S H ⊥ A B C
A H = 2 3 a 3 2 = a 3 3 S H = S A 2 − A H 2 = 3 a 2 − a 2 3 = 2 6 a 3 V S . A B C = 1 3 S H . S A B C = 1 3 2 6 a 3 a 2 3 4 = a 3 2 6

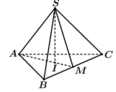
Gọi I là tâm đường tròn ngoại tiếp tam giác ABC. Vì S.ABC là khối chóp đều nên suy ra S I ⊥ ( A B C )
Gọi M là trung điểm của BC
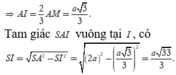
Diện tích tam giác ABC là: ![]()
Vậy thể tích khối chóp ![]()
Chọn C.

Đáp án D
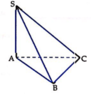
Do Δ A B C đều có cạnh bằng 2a nên
S Δ A B C = 2 a 2 . 3 4 = a 2 3 (đvdt).
Thể tích khối chóp S.ABC là: V S . A B C = 1 3 S A . S Δ A B C = 1 3 . a 3 . a 2 3 = a 3
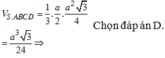
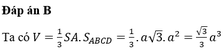
Đáp án B
A M = 4 a 2 − a 2 = a 3 ⇒ A G = 2 3 3 a
S G = 3 a 2 − 4 3 a 2 = 15 3 a V = 1 3 . 15 3 a . 1 2 . a 3 .2 a = 5 a 3 3