
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta chia khối lẳng trụ đã cho thành hình chóp A’.ABC, C.A’B’C’ và C.A’BB’
Ta có: VA’.ABC = VA’B’C’ = 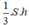 trong đó S là diện tích đáy S = SABC = SA’B’C’ và h là chiều cao của hình lăng trụ
trong đó S là diện tích đáy S = SABC = SA’B’C’ và h là chiều cao của hình lăng trụ
Lại có: VABC.A’B’C’ = S.h
Do đó,
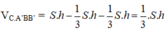
Trong đó, tam giác ABC là tam giác đều có độ dài cạnh bằng a nên 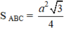
Vì đây là hình lăng trụ đứng nên h = AA’ = BB’= CC’ = a.
Vậy thể tích hình chóp C.A’BB’ là:
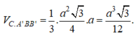

Đáp án D
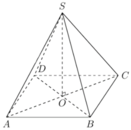
Gọi khối chóp tứ giác đều đó là S. ABCD.
Gọi O là giao điểm hai đường chéo hình vuông ABCD, ta có SO là đường cao hình chóp.
S O = S A 2 - A O 2 = a 2 - a 2 2 2 = a 2 2
S A B C D = a 2
Vậy thể tích cần tìm là:
V = 1 3 . S A B C D . S O = 1 3 a 2 . a 2 2 = a 3 2 6

Đáp án A
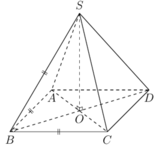
Diện tích đáy ABCD là a2.
Ta có
S O 2 = S B 2 - O B 2 = a 2 - a 2 2 2 = a 2 2
Suy ra S O = a 2 2
Thể tích khói chóp cần tìm là
V = 1 3 . a 2 2 . a 2 = a 3 2 6

Chọn C.
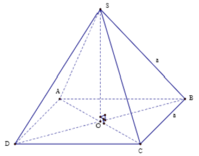
Gọi khối chóp tứ giác đều là S.ABCD
Gọi O là tâm của đáy Do là khối chóp tứ giác đều nên SO ⊥ (ABCD)
Vậy SO là chiều cao của khối chóp S.ABCD.
Xét tam giác vuông SOB, ta có:
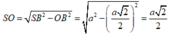
Thể tích khối chóp là:
![]()