Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có : \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=120+90+\widehat{C}+\widehat{D}=360^o\)
\(\Rightarrow\widehat{C}+\widehat{D}=150^o\)
Mà \(\widehat{C}=2\widehat{D}\)
\(\Rightarrow\left\{{}\begin{matrix}\widehat{C}=100\\\widehat{D}=50\end{matrix}\right.\)
Vậy ...
Ta có:
\(A+B+C+D=360^0\)
\(\Leftrightarrow120^0+90^0+2D+D=360^0\)
\(\Leftrightarrow3D=150^0\)
\(\Rightarrow D=50^0\)
\(C=2D=100^0\)

Ta có: ∠A + ∠B + ∠C + ∠D = 360o
⇒ 120o + 90o + ∠C + ∠D = 360o
⇒ ∠C + ∠D = 150o
Lại có: ∠C = 2∠D
⇒ 2∠D + ∠D = 150o
⇒ 3∠D = 150o
⇒ ∠D = 50o
∠C = ∠D.2 = 50o/2 = 100o
∠D = 100o/2 = 50o

Góc ngoài tại đỉnh A có số đo là:
\(180^0-75^0=105^{ }\)
Góc ngoài tại đỉnh B có số đo là:
\(180^0-90^0=90^0\)
Góc ngoài tại đỉnh C có số đo là:
\(180^0-120^0=60^0\)
Góc ngoài tại đỉnh D có số đo là:
\(180^0-75^0=105^{ }\)

a) Ta thấy : A + B + C + D = 360°
Tự áp dụng tính chất dãy tỉ số bằng nhau ta có :
A = 144°
B = 108°
C = 72°
D = 36°
b) Vì DE , CE là phân giác ADC và ACD
=> EDC = ADE = 18°
=> BCE = ECD = 36°
Xét ∆DEC ta có :
EDC + DEC + ECD = 180°
=> DEC = 126°
Ta có : góc ngoài tại đỉnh C
=> 180° - BCD = 108°
Góc ngoài tại đỉnh D
=> 180° - ADC = 144°
Mà DF , CF là phân giác ngoài góc C , D
=> CDF = 72°
=> DCF = 54°
Xét ∆CDF ta có :
CDF + DFC + DCF = 180°
=> DFC = 44°

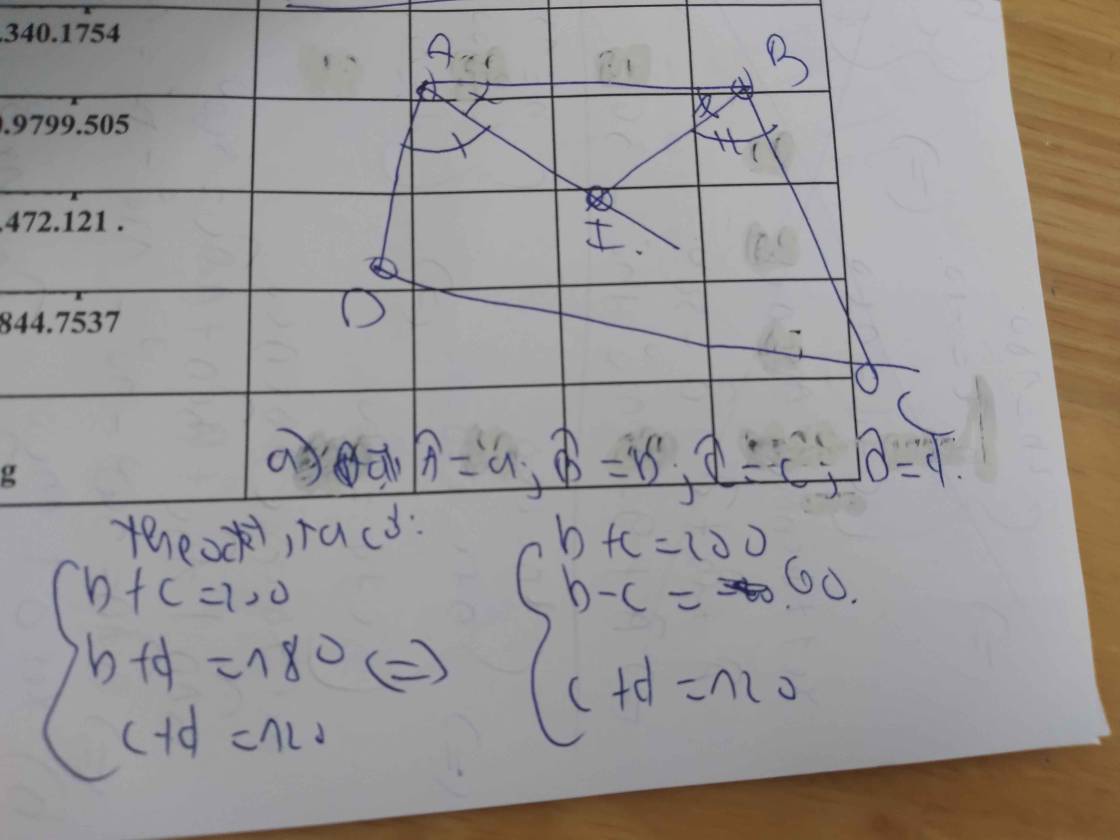
1. Áp dụng định lý tổng 3 góc vào tam giác ICD , bạn tính được góc ICD +góc IDC = 75 độ
Mà góc BCD = 2 góc ICD và góc ADC = 2 góc IDC nên góc BCD + góc ADC = 2.75 = 150 độ
Xét tứ giác ABCD có: góc A + góc B + góc BCD + góc ADC = 360 độ
góc A + 90 độ + 150 độ = 360 độ
góc A = 120 độ
2. góc C của tứ giác là: 180 độ -130 độ = 50 độ
Chúc bạn học tốt.

Tứ giác ABCD là hình thang vuông
Ta có B = C = 90*
=> B + C = 180*
=> A + D = 180* ( Vì tứ giác có 360 độ )
=> 8x + 6 + 3x + 9 = 180
<=> 11x + 15 =180
<=> 11x = 180 - 15 = 165*
x = 165 : 11 =15
=> A = 8 x 15 + 6 = 126*
D = 3 X 15 + 9 = 54
Vậy ....


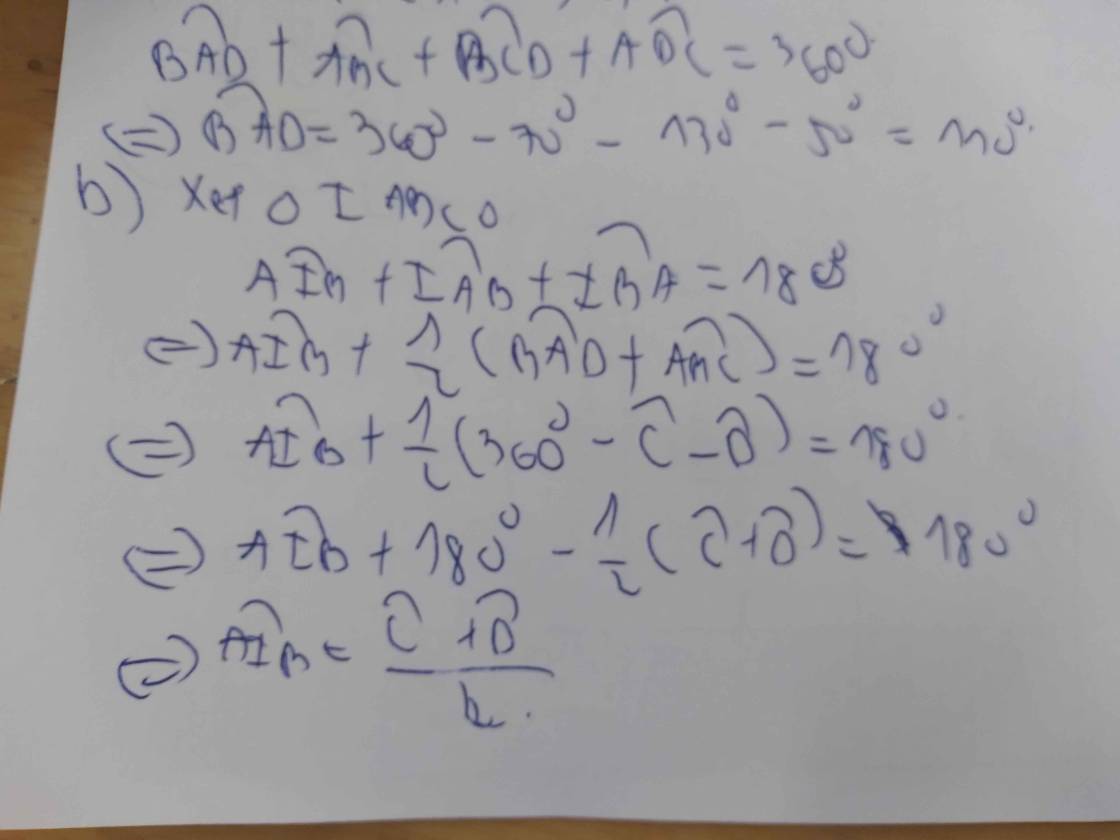
D ^ = 50 0 , C ^ = 100 0