
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\frac{1}{12}-\left(-\frac{1}{6}-\frac{1}{4}\right)\)
\(=\frac{1}{12}-\left(-\frac{2}{12}-\frac{3}{12}\right)\)
\(=\frac{1}{12}+\frac{2}{12}+\frac{3}{12}\)
\(=\frac{1}{2}\)
Thanks bạn cute Jeon Koo Koo nhìu nha , tớ cảm ơn pạn rất nhìu :3


a: \(M=\left|x\right|+x\)
\(=\left[{}\begin{matrix}x+x=2x\left(x\ge0\right)\\-x+x=0\left(x< 0\right)\end{matrix}\right.\)
b: \(N=\left|x\right|:x=\pm1\)

a) Ta có: a⊥c,b⊥c
=> a//b
b) Ta có: a//b
\(\Rightarrow\widehat{B_1}+\widehat{A_1}=180^0\)(trong cùng phía)
\(\Rightarrow\widehat{B_1}=180^0-120^0=60^0\)
c) Ta có: \(\widehat{A_1}=\widehat{B_2}\)(2 góc so le trong và a//b)
\(\Rightarrow\widehat{A_2}+\widehat{B_2}=\widehat{A_2}+\widehat{A_1}=180^0\)(kề bù)

a) Do \(\left(3x-\dfrac{1}{2}\right)^2\ge0\forall x\)
\(\Rightarrow A=\left(3x-\dfrac{1}{2}\right)^2-4\ge-4\)
\(minA=-4\Leftrightarrow x=\dfrac{1}{6}\)
b) Do \(\left(2x+1\right)^4\ge0\forall x,\left(y-\dfrac{1}{2}\right)^6\ge0\forall y\)
\(\Rightarrow B=\left(2x+1\right)^4+3\left(y-\dfrac{1}{2}\right)^6\ge0\)
\(minB=0\Leftrightarrow\)\(\left\{{}\begin{matrix}x=-\dfrac{1}{2}\\y=\dfrac{1}{2}\end{matrix}\right.\)
a: \(A=\left(3x-\dfrac{1}{2}\right)^2-4\ge-4\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{1}{6}\)
b: \(B=\left(2x+1\right)^4+3\left(y-\dfrac{1}{2}\right)^6\ge0\forall x,y\)
Dấu '=' xảy ra khi \(\left(x,y\right)=\left(-\dfrac{1}{2};\dfrac{1}{2}\right)\)

câu 5: đáp án là C nhé bạn
Câu 6: Căn bậc hai số học của 25 là: 5 -5 cộng trừ 5 225

a: Áp dụng tính chất của dãy tỉ số bằng nhau,ta được:
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{5}=\dfrac{x+y+z}{2+3+5}=\dfrac{-90}{10}=-9\)
Do đó: x=-18; y=-27; z=-45
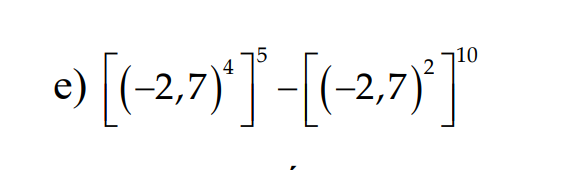
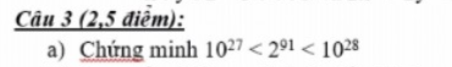
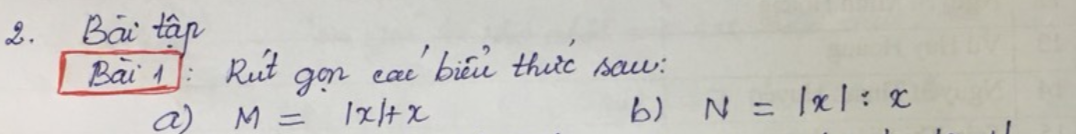 giúp mình câu này nhanh với ạ
giúp mình câu này nhanh với ạ

 giúp mình 2 câu này với ạ mình đang cần gấp
giúp mình 2 câu này với ạ mình đang cần gấp
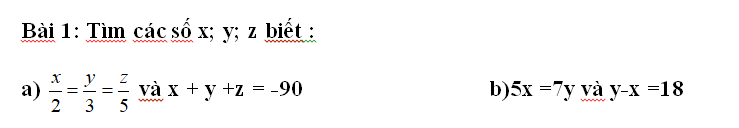 tìm giúp mình 2 câu này với ạ
tìm giúp mình 2 câu này với ạ
\(=\left(-2,7\right)^{20}-\left(-2,7\right)^{20}=0\)