NN
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
22 tháng 1 2023
Câu 1: x^3+y^3+3xy
=(x+y)^3-3xy(x+y)+3xy
=(x+y)^3-3xy+3xy
=1
Câu 2:
x^3-y^3-3xy
=(x-y)^3+3xy(x-y)-3xy
=1^3
=1
Câu 3:
\(x^2+y^2=\left(x+y\right)^2-2xy=4-2\cdot\left(-15\right)=4+30=34\)
Câu 4:
\(x^3+y^3=\left(x+y\right)^3-3xy\left(x+y\right)=-8-3\cdot\left(-2\right)\cdot\left(-15\right)=-8-3\cdot30=-98\)
Câu 5: B
Câu 6: C
Câu 7: B
Câu 8: D
Câu 10: B
NB
23 tháng 1 2023
1) Nếu x+y=1, thì giá trị của biểu thức x3+y3+3xy là
A.2
B.3
C.4
D.cả A,B,C đều sai
2)Nếu x-y=1, thì giá trị của biểu thức x3-y3-3xy là
A.1
B.2
C.3
D.4
3) Cho x+y= -2, xy=-15 thì giá trị của biểu thức x2+y2 là.
A) 30 ; B) 32 ;C) 28 ; D) Cả A và B đều sai.
4) Với giả thiết bài 3, ta có giá trị của biểu thức x3+y3 là:
A) 80 ; B) 81; C) 82 ; D) Một kết quả khác
5) Với giả thiết bài 3, ta có giá trị của biểu thức x4+y4 là:
A. 706 ; B. 702 ; C. 708 ; D. 704
6)Giá trị nhỏ nhất của biểu thức P= x(x+1)(x+2)(x+3) là
A. 1 ; B. 2 ; C. -1 ; D.-2
7)Cho biểu thức M=2x2+9y2- 6xy-6x-12y+2037 . Giá trị nhỏ nhất của biểu thức M là
A. 2007 ; B. 2008 ; C; 2009 ; D. 2010
8) Với giả thiết bài 7 , biểu thức M đạt giá trị nhỏ nhất khi
A)x=5;y= 7/3
B)x= -5; y= 7/3
C) x=5; y= -7/3
D)cả A và C đều sai
9) Cho biểu thức Q= 2xy+6x-2y-2x2-y2+ 2015 .Giá trị lớn nhất của biểu thức Q là
A. 2010 ; B. 2012 ; C. 2020 ; D. Một kết quả khác
NH
2
11 tháng 8 2021
a) Ta có: \(M=x^2-2xy+y^2-10x+10y\)
\(=\left(x-y\right)^2-10\left(x-y\right)\)
\(=9^2-10\cdot9=-9\)
15 tháng 10 2023
a) \(A=x^3+y^3+3xy\)
\(=x^3+y^3+3xy\left(x+y\right)\) (do \(x+y=1\))
\(=x^3+3x^2y+3xy^2+y^3\)
\(=\left(x+y\right)^3\) \(=1\)
b) \(B=x^3-y^3-3xy\)
\(=x^3-y^3-3xy\left(x-y\right)\) (do \(x-y=1\))
\(=x^3-3x^2y+3xy^2-y^3\)
\(=\left(x-y\right)^3\) \(=1\)
3 tháng 10 2023
`#3107.101107`
`D = x^3 - y^3 - 3xy` biết `x - y - 1 = 0`
Ta có:
`x - y - 1 = 0`
`=> x - y = 1`
`D = x^3 - y^3 - 3xy`
`= (x - y)(x^2 + xy + y^2) - 3xy`
`= 1 * (x^2 + xy + y^2) - 3xy`
`= x^2+ xy + y^2 - 3xy`
`= x^2 - 2xy + y^2`
`= x^2 - 2*x*y + y^2`
`= (x - y)^2`
`= 1^2 = 1`
Vậy, với `x - y = 1` thì `D = 1`
________
`E = x^3 + y^3` với `x + y = 5; x^2 + y^2 = 17`
`x + y = 5`
`=> (x + y)^2 = 25`
`=> x^2 + 2xy + y^2 = 25`
`=> 2xy = 25 - (x^2 + y^2)`
`=> 2xy = 25 - 17`
`=> 2xy = 8`
`=> xy = 4`
Ta có:
`E = x^3 + y^3`
`= (x + y)(x^2 - xy + y^2)`
`= 5 * [ (x^2 + y^2) - xy]`
`= 5 * (17 - 4)`
`= 5 * 13`
`= 65`
Vậy, với `x + y = 5; x^2 + y^2 = 17` thì `E = 65`
________
`F = x^3 - y^3` với `x - y = 4; x^2 + y^2 = 26`
Ta có:
`x - y = 4`
`=> (x - y)^2 = 16`
`=> x^2 - 2xy + y^2 = 16`
`=> (x^2 + y^2) - 2xy = 16`
`=> 2xy = (x^2 + y^2) - 16`
`=> 2xy = 26 - 16`
`=> 2xy = 10`
`=> xy = 5`
Ta có:
`F = x^3 - y^3`
`= (x - y)(x^2 + xy + y^2)`
`= 4 * [ (x^2 + y^2) + xy]`
`= 4 * (26 + 5)`
`= 4*31`
`= 124`
Vậy, với `x - y = 4; x^2 + y^2 = 26` thì `F = 124.`
15 tháng 7 2021
B1
a, \(=>A=\left(x+y+x-y\right)\left(x+y-x+y\right)=2x.2y=4xy\)
b, \(=>B=\left[\left(x+y\right)-\left(x-y\right)\right]^2=\left[x+y-x+y\right]^2=\left[2y\right]^2=4y^2\)
c,\(\left(x^2+x+1\right)\left(x^2-x+1\right)\left(x^2-1\right)\)
\(=\)\(\left(x+1\right)\left(x^2-x+1\right)\left(x-1\right)\left(x^2+x+1\right)=\left(x^3+1^3\right)\left(x^3-1^3\right)=x^6-1\)
d, \(\left(a+b-c\right)^2+\left(a-b+c\right)^2-2\left(b-c\right)^2\)
\(=\left(a+b-c\right)^2-\left(b-c\right)^2+\left(a-b+c\right)^2-\left(b-c\right)^2\)
\(=\left(a+b-c+b-c\right)\left(a+b-c-b+c\right)\)
\(+\left(a-b+c+b-c\right)\left(a-b+c-b+c\right)\)
\(=a\left(a+2b-2c\right)+a\left(a-2b\right)\)
\(=a\left(a+2b-2c+a-2b\right)=a\left(2a-2c\right)=2a^2-2ac\)
B2:
\(\)\(x+y=3=>\left(x+y\right)^2=9=>x^2+2xy+y^2=9\)
\(=>xy=\dfrac{9-\left(x^2+y^2\right)}{2}=\dfrac{9-\left(17\right)}{2}=-4\)
\(=>x^3+y^3=\left(x+y\right)\left(x^2-xy+y^2\right)=3\left(17+4\right)=63\)
15 tháng 7 2021
Bài 1:
a) Ta có: \(\left(x+y\right)^2-\left(x-y\right)^2\)
\(=x^2+2xy+y^2-x^2+2xy+y^2\)
=4xy
b) Ta có: \(\left(x+y\right)^2-2\left(x+y\right)\left(x-y\right)+\left(x-y\right)^2\)
\(=\left(x+y-x+y\right)^2\)
\(=\left(2y\right)^2=4y^2\)
c) Ta có: \(\left(x^2+x+1\right)\left(x^2-x+1\right)\left(x^2-1\right)\)
\(=\left(x-1\right)\left(x^2+x+1\right)\left(x+1\right)\left(x^2-x+1\right)\)
\(=\left(x^3-1\right)\left(x^3+1\right)\)
\(=x^6-1\)
d) Ta có: \(\left(a+b-c\right)^2+\left(a+b+c\right)^2-2\left(b-c\right)^2\)
\(=\left(a+b-c\right)^2-\left(b-c\right)^2+\left(a+b+c\right)^2-\left(b-c\right)^2\)
\(=\left(a+b-c-b+c\right)\left(a+b-c+b-c\right)+\left(a+b+c-b+c\right)\left(a+b+c+b-c\right)\)
\(=a\cdot\left(a+2b-2c\right)+\left(a+2c\right)\left(a-2b\right)\)
\(=a^2+2ab-2ac+a^2-2ab+2ac-4bc\)
\(=2a^2-4bc\)
T
15 tháng 10 2023
\(a,A=x^2+y^2\\=x^2-2xy+y^2+2xy\\=(x-y)^2+2xy\\=2^2+2\cdot1\\=4+2\\=6\)
\(b,x+y=1\\\Leftrightarrow (x+y)^3=1^3\\\Leftrightarrow x^3+3x^2y+3xy^2+y^3=1\\\Leftrightarrow x^3+3xy(x+y)+y^3=1\\\Leftrightarrow x^3+3xy\cdot1+y^3=1\\\Rightarrow A=1\)
H9
HT.Phong (9A5)
CTVHS
15 tháng 10 2023
a) Ta có:
\(x-y=2\)
\(\Rightarrow\left(x-y\right)^2=2^2\)
\(\Rightarrow x^2-2xy+y^2=4\)
Mà: \(xy=1\)
\(\Rightarrow\left(x^2+y^2\right)-2\cdot1=4\)
\(\Rightarrow x^2+y^2=4+2\)
\(\Rightarrow x^2+y^2=6\)
b) Ta có:
\(x+y=1\)
\(\Rightarrow\left(x+y\right)^3=1^3\)
\(\Rightarrow x^3+3x^2y+3xy+y^3=1\)
\(\Rightarrow x^3+3xy\left(x+y\right)+y^3=1\)
Mà: x + y = 1
\(\Rightarrow x^3+3xy\cdot1+y^3=1\)
\(\Rightarrow x^3+3xy+y^3=1\)
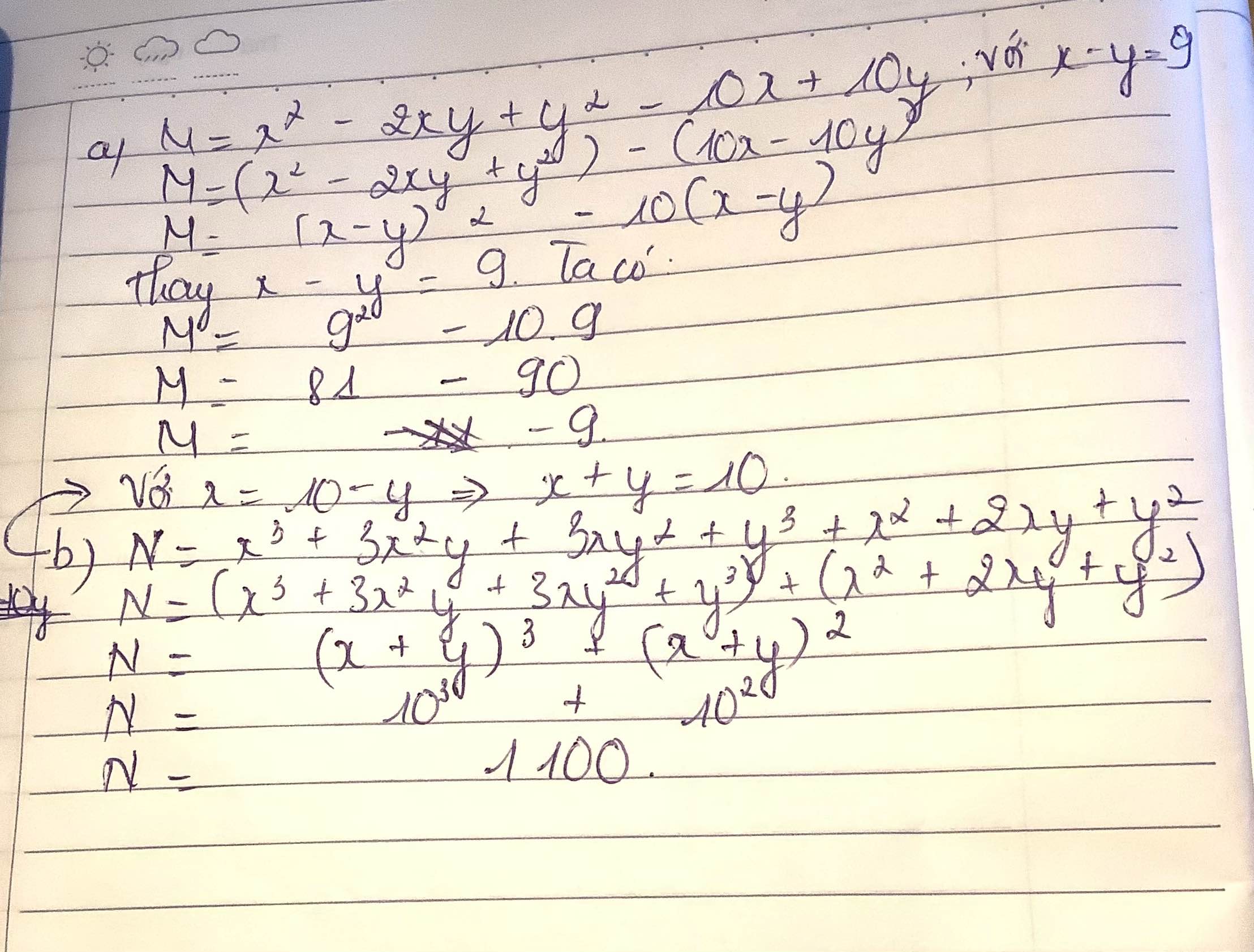
a) Ta có: \(y-x=1\Rightarrow x-y=-1\)
\(A=x^3-y^3+3xy\)
\(A=\left(x-y\right)\left(x^2+xy+y^2\right)+3xy\)
\(A=-x^2-xy-y^2+3xy\)
\(A=-\left(x-y\right)^2=-\left(-1\right)^2=-1\)
b) Ta có:
\(B=x\left(x+2\right)+y\left(y-2\right)-2xy+37\)
\(B=x^2+2x+y^2-2y-2xy+37\)
\(B=\left(x^2-2xy+y^2\right)+2\left(x-y\right)+1+36\)
\(B=\left(x-y\right)^2+2\left(x-y\right)+1+36\)
\(B=\left(x-y+1\right)^2+36\)
\(B=11^2+36=121+36=157\)