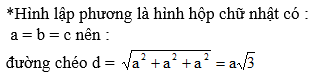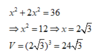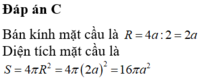Tính độ dài đường chéo của một hình lập phương cạnh a ?

K

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

SG

Sách Giáo Khoa

31 tháng 3 2017

Tính độ dài đường chéo của một hình lập phương cạnh a ?

#Toán lớp 11

1

QD

Quang Duy

31 tháng 3 2017

Giải bài 8 trang 114 sgk Hình học 11 | Để học tốt Toán 11

Các câu hỏi dưới đây có thể giống với câu hỏi trên

PT

Pham Trong Bach

8 tháng 10 2017

Tính độ dài đường chéo của một hình lập phương cạnh a.

#Toán lớp 11

1

CM

Cao Minh Tâm

8 tháng 10 2017

+ Hình lập phương là hình hộp chữ nhật với a = b = c.

Áp dụng kết quả bài 7b) ta có:

Độ dài đường chéo hình lập phương là:

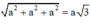
Giải bài 8 trang 114 sgk Hình học 11 | Để học tốt Toán 11

B

Buddy

14 tháng 8 2023

Cho hình lập phương có cạnh bằng a. Tính độ dài đường chéo của hình lập phương đó.

#Toán lớp 11

1

NL

Nguyễn Lê Phước Thịnh

14 tháng 8 2023

ΔABC vuông tại B

=>\(AC=\sqrt{AB^2+BC^2}=a\sqrt{2}\)

ΔA'AC vuông tại A

=>\(A'C=\sqrt{A'A^2+AC^2}=a\sqrt{3}\)

=>Độ dài đường chéo là \(a\sqrt{3}\)

B

Buddy

16 tháng 8 2023

Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a.a) Tính độ dài đường chéo của hình lập phương.b) Chứng minh rằng (ACC′A′) \( \bot \) (BDD′B′).c) Gọi O là tâm của hình vuông ABCD. Chứng minh rằng \(\widehat {COC'}\) là một góc phẳng của góc nhị diện [C, BD, C']. Tính (gần đúng) số đo của các góc nhị diện [C, BD, C'], [A, BD,...

#Toán lớp 11

1

QT

Quoc Tran Anh Le

Giáo viên

22 tháng 9 2023

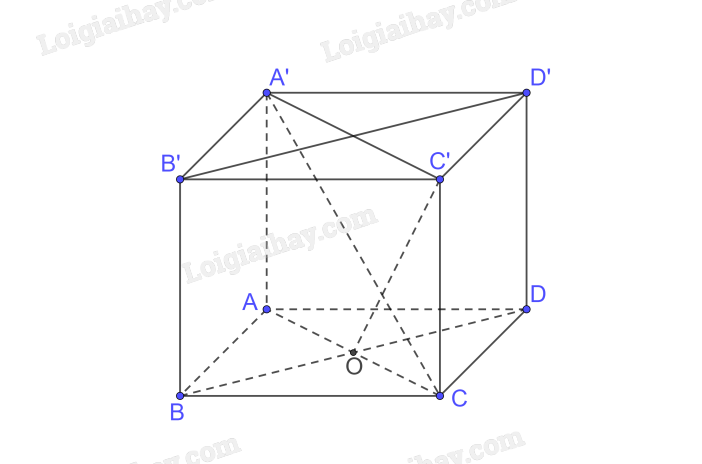
loading...

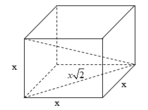
a) Xét tam giác ABC vuông tại B có

\(A{C^2} = A{B^2} + B{C^2} = {a^2} + {a^2} = 2{a^2} \Rightarrow AC = a\sqrt 2 \)

Xét tam giác AA’C vuông tại A có

\(A'{C^2} = A{A'^2} + A{C^2} = {a^2} + {\left( {a\sqrt 2 } \right)^2} = 3{a^2} \Rightarrow A'C = a\sqrt 3 \)

Vậy độ dài đường chéo hình lập phương bằng \(a\sqrt 3 \)

b) Ta có \(\begin{array}{l}BD \bot AC,BD \bot AA' \Rightarrow BD \bot \left( {ACC'A'} \right);BD \subset \left( {BDD'B'} \right)\\ \Rightarrow \left( {ACC'A'} \right) \bot \left( {BDD'B'} \right)\end{array}\)

c) Ta có \(C'O \bot BD\left( {BD \bot \left( {ACC'A'} \right)} \right),CO \bot BD \Rightarrow \left[ {C,BD,C'} \right] = \left( {CO,C'O} \right) = \widehat {COC'}\)

\(OC = \frac{{AC}}{2} = \frac{{a\sqrt 2 }}{2}\)

Xét tam giác COC’ vuông tại C có

\(\tan \widehat {COC'} = \frac{{CC'}}{{OC}} = \frac{a}{{\frac{{a\sqrt 2 }}{2}}} = \sqrt 2 \Rightarrow \widehat {COC'} = \arctan \sqrt 2 \)

Ta có \(C'O \bot BD\left( {BD \bot \left( {ACC'A'} \right)} \right),AO \bot BD \Rightarrow \left[ {A,BD,C'} \right] = \left( {AO,C'O} \right) = \widehat {AOC'}\)

\(\widehat {AOC'} = {180^0} - \widehat {COC'} \approx 125,{26^0}\)

PT

Pham Trong Bach

26 tháng 10 2018

Tính thể tích V của hình lập phương có độ dài đường chéo bằng 6

A. V = 24 3

B. V = 8 3

C. V = 4 3

D. V = 12 3

#Toán lớp 11

1

CM

Cao Minh Tâm

26 tháng 10 2018

Đáp án A

PT

Pham Trong Bach

6 tháng 11 2017

Một khối lập phương có độ dài đường chéo bằng a 6 Tính thể tích của khối lập phương đó. ...

#Toán lớp 11

1

CM

Cao Minh Tâm

6 tháng 11 2017

PT

Pham Trong Bach

8 tháng 2 2018

Tính diện tích mặt cầu ngoại tiếp hình lập phương có độ dài đường chéo bằng 4a

#Toán lớp 11

1

CM

Cao Minh Tâm

8 tháng 2 2018

PT

Pham Trong Bach

25 tháng 1 2017

Cho hình lập phương ABCD.A’B’C’D’ cạnh a.

a) Chứng minh rằng đường thẳng AC’ vuông góc với mặt phẳng (A’BD) và mặt phẳng (ACC’A’) vuông góc với mặt phẳng (A’BD).

b) Tính đường chéo AC’ của hình lập phương đã cho.

#Toán lớp 11

1

CM

Cao Minh Tâm

25 tháng 1 2017

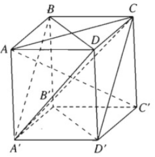
Giải sách bài tập Toán 11 | Giải sbt Toán 11

a) Ta có AB = AD = AA′ = a

và C ′ B = C ′ D = C ′ A ′ = a 2

Vì hai điểm A và C’ cách đều ba đỉnh của tam giác A’BD nên A và C’ thuộc trục đường tròn ngoại tiếp tam giác BDA’ . Vậy AC′ ⊥ (BDA′). Mặt khác vì mặt phẳng (ACC’A’) chứa đường thẳng AC’ mà AC′ ⊥ (BDA′) nên ta suy ra mặt phẳng (ACC’A’) vuông góc với mặt phẳng (BDA’)

b) Ta có ACC’ là tam giác vuông có cạnh A C = a 2 và CC’ = a

Vậy A C ′ 2 = A C 2 + C C ′ 2

⇒ A C ′ 2 = 2 a 2 + a 2 = 3 a 2 . V ậ y A C ′ = a 3 .

PT

Pham Trong Bach

13 tháng 5 2019

Cho một hình hộp có độ dài ba cạnh cùng xuất phát từ một đỉnh lần lượt là 3,4,5. Tổng bình phương tất cả các đường chéo của hình hộp đó bằng:

A. 50

B. 60

C. 200

D. Không tính được

#Toán lớp 11

1

CM

Cao Minh Tâm

13 tháng 5 2019

Đáp án C

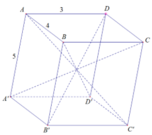
(Dễ dàng chứng minh định lý: trong hình bình hành, tổng bình phương 2 đường chéo bằng tổng bình phương các cạnh bằng định lý hàm cos)

Ta có: A C ' 2 = A A ' 2 + A ' C ' 2

= A A ' 2 + A ' D ' 2 + A ' B ' 2

= 50

Tương tự BD’=AC’=DB’=CA’=50

SG

Sách Giáo Khoa

22 tháng 5 2017

a) Cho hình lập phương ABCD. A'B'C'D' cạnh a. Chứng minh rằng đường thẳng AC' vuông góc với mặt phẳng (A'BD) và mặt phẳng (ACC'A') vuông góc với mặt phẳng (A'BD)

b) Tính đường chéo AC' của hình lập phương đã cho

#Toán lớp 11

1

NT

Nguyen Thuy Hoa

26 tháng 5 2017

Vectơ trong không gian, Quan hệ vuông góc

b) Ta có ACC' là tam giác vuông có cạnh \(AC=a\sqrt{2},CC'=a\)

Vậy \(AC'^2=AC^2+CC^2\Rightarrow AC'^2=2a^2+a^2=3a^2\)

Vậy \(AC'=a\sqrt{3}\)