Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi a, b, c lần lượt là các cạnh của tam giác ấy (a, b, c \(\in\) N*)
Theo tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}\Rightarrow\frac{a+b+c}{3+4+5}=\frac{24}{12}=2\)
=> \(\frac{a}{3}=\)2 \(\Rightarrow\) a=2.3=6
=> \(\frac{b}{4}=2\Rightarrow b=2.4=8\)
=> \(\frac{c}{5}=2\Rightarrow c=2.5=10\)
Vậy các cạnh của tam giác lần lượt bằng 6 cm ,8 cm ,10 cm
Giải:
Gọi các cạnh của tam giác lần lượt là a, b, c \(\left(a,b,c>0\right)\)
Ta có: \(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}\) và a + b + c = 24
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}=\frac{a+b+c}{3+4+5}=\frac{24}{12}=2\)
+) \(\frac{a}{3}=2\Rightarrow a=6\)
+) \(\frac{b}{4}=2\Rightarrow b=8\)
+) \(\frac{c}{5}=2\Rightarrow10\)
Vậy ba cạnh của tam giac lần lượt là 6, 8, 10

Gọi độ dài các cạnh của tam giác đó lần lượt là a;b;c (a;b;c > 0)
Ta có \(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}\); a + b + c = 36
Áp dụng tính chất dãy tỉ số bằng nhau là
\(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}=\frac{a+b+c}{3+4+5}=\frac{36}{12}=3\)
=> a = 3.3 = 9; b = 3.4 = 12; c = 3.5 = 15
Vậy độ dài các cạnh của tam giác lần lượt là 9;12;15 cm
Gọi a,b,c lần lượt là độ dài các cạnh của tam giác
Ta có : \(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}\)và a + b + c = 36.
Áp dụng tính chất dãy tỉ số bằng nhau
\(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}=\frac{a+b+c}{3+4+5}=\frac{36}{12}=3\)
\(\frac{a}{3}=3\Rightarrow a=3.3=9\)
\(\frac{b}{4}=3\Rightarrow b=4.3=12\)
\(\frac{c}{5}=3\Rightarrow c=5.3=15\)
Vậy độ dài các cạnh lần lượt là 9 ; 12 ; 15.

Gọi độ dài các cạnh của tam giác lần lượt là a; b ; c ( đk : 0 < a;b;c < 13,2 )
Theo bài ra ta có : a/3=b/4=c/5 và a+b+c=13,2
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
a/3=b/4=c/5=a+b+c/3+4+5=13,2/12=1,1
+, a/3=1,1 => a=3,3 ( tm)
+, b/4=1,1 => b=4,4 ( tm )
+, c/5=1,1 => c=5,5 ( tm )
Vậy độ dài của các cạnh của tam giác là 3,3 ; 4,4 ; 5,5 (cm ).

Gọi x , y , z lần lượt là độ dài các cạnh của tam giác (cm) ( x , y , z > 0 )
Chu vi của tam giác là 36 cm nên x + y + z = 36
Vì các cạnh của tam giác tỉ lệ với các số 3 , 4 , 5 nên x/3 =y/4 = z/5
Theo tính chất dãy tỉ số bằng nhau ta có :
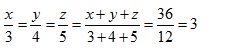
Suy ra : x = 3 . 3 = 9 (TM)
y = 4 . 3 = 12 (TM)
z = 5 . 3 = 15 (TM)
Vậy độ dài các cạnh của tam giác lần lượt là : 9cm , 12cm , 15cm .

Gọi độ dài ba cạnh lần lượt là a,b,c
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{2}=\dfrac{b}{4}=\dfrac{c}{5}=\dfrac{a+b+c}{2+4+5}=\dfrac{22}{11}=2\)
Do đó: a=4; b=8; c=10
gọi các cạnh của tam giác lần lượt là x,y,z
=>\(\frac{x}{3}=\frac{y}{4}=\frac{z}{5}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta đc
\(\frac{x}{3}=\frac{y}{4}=\frac{z}{5}=\frac{x+y+z}{3+4+5}=\frac{24}{12}=2\)
=>x=2.3=6
y=2.4=8
z=2.5=10
Vậy các cạnh của tam giác lần lượt là 6,8,10
Gọi độ dài các cạnh trong tam giác lần lượt là \(a;b;c\left(a;b;c\in N\text{*}\right)\left(cm\right)\)
\(\text{Theo bài ra ta có: }a+b+c=24\\ \dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta được :
\(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}=\dfrac{a+b+c}{3+4+5}=\dfrac{24}{12}=2\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{a}{3}=2\\\dfrac{b}{4}=2\\\dfrac{c}{5}=2\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a=6\\b=8\\c=10\end{matrix}\right.\)
Vậy \(a=6;b=8;c=10\)
\(\)
\(\)