
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Từ f ( x ) + f x + π 2 = sin x + cos x cho x = π 2 , x = - π 2 ta có
f π 2 + f π 2 + π 2 = sin π 2 + cos π 2 = sin π 2 f - π 2 + f π 2 - π 2 = sin - π 2 + cos π 2 = sin π 2
Chú ý do y = f x + π 2 là hàm chẵn trên - π 2 ; π 2 nên f π 2 + π 2 = f π 2 - π 2
⇒ f π 2 - f - π 2 = sin π 2 - sin - π 2 ⇒ f ( x ) = sin x
Vậy ∫ 0 π 2 f ( x ) d x = ∫ 0 π 2 sin x = 1
Đáp án cần chọn là B

Đáp án C
∫ 0 π 2 sin x − cos x d x = − ∫ 0 π 4 sin x − cos x d x + ∫ π 4 π 2 sin x − cos x d x = − 2 ∫ 0 π 4 sin x − π 4 d x + ∫ π 4 π 2 sin x − π 4 d x S = 2 . cos x − π 4 π 4 0 − 2 . cos x − π 4 π 2 π 4 = 2 1 − 1 2 − 2 1 2 − 1 = 2 2 − 2 = 2 2 − 1
“Dùng CASIO tính tích phân trị tuyệt đối, dò đáp án
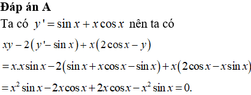

ta có
\(y'=\left(cosx-sinx\right)e^x+\left(sinx+cosx\right)e^x=2.cosx.e^x\)
Bla bla, spam tự hỏi tự trả lời nha!