Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta có y = 4 sin 2 x + 2 sin 2 x + π 4 = 4 1 − cos 2 x 2 + sin 2 x + cos 2 x
= sin 2 x − cos 2 x + 2 = 2 sin 2 x − π 4 + 2.
Mà − 1 ≤ sin 2 x − π 4 ≤ 1 ⇒ − 2 + 2 ≤ 2 sin 2 x − π 4 + 2 ≤ 2 + 2
Vậy giá trị lớn nhất của hàm số là 2 + 2 .
Chọn đáp án D.
Ta có y = 4 sin 2 x + 2 sin 2 x + π 4 = 4 1 − cos 2 x 2 + sin 2 x + cos 2 x
= sin 2 x − cos 2 x + 2 = 2 sin 2 x − π 4 + 2.
Mà − 1 ≤ sin 2 x − π 4 ≤ 1 ⇒ − 2 + 2 ≤ 2 sin 2 x − π 4 + 2 ≤ 2 + 2
Vậy giá trị lớn nhất của hàm số là 2 + 2 .
Chọn đáp án D.
1:
a: ĐKXĐ: \(x< >\dfrac{\Omega}{2}+k\Omega\)
=>TXĐ: \(D=R\backslash\left\{\dfrac{\Omega}{2}+k\Omega\right\}\)
b: ĐKXĐ: \(x< >k\Omega\)
=>TXĐ: \(D=R\backslash\left\{k\Omega\right\}\)
c: ĐKXĐ: \(2x< >\dfrac{\Omega}{2}+k\Omega\)
=>\(x< >\dfrac{\Omega}{4}+\dfrac{k\Omega}{2}\)
TXĐ: \(D=R\backslash\left\{\dfrac{\Omega}{4}+\dfrac{k\Omega}{2}\right\}\)
d: ĐKXĐ: \(3x< >\Omega\cdot k\)
=>\(x< >\dfrac{k\Omega}{3}\)
TXĐ: \(D=R\backslash\left\{\dfrac{k\Omega}{3}\right\}\)
e: ĐKXĐ: \(x+\dfrac{\Omega}{3}< >\dfrac{\Omega}{2}+k\Omega\)
=>\(x< >\dfrac{\Omega}{6}+k\Omega\)
TXĐ: \(D=R\backslash\left\{\dfrac{\Omega}{6}+k\Omega\right\}\)
f: ĐKXĐ: \(x-\dfrac{\Omega}{6}< >\Omega\cdot k\)
=>\(x< >k\Omega+\dfrac{\Omega}{6}\)
TXĐ: \(D=R\backslash\left\{k\Omega+\dfrac{\Omega}{6}\right\}\)
Đặt \(sinx=t\in\left[-1;1\right]\)
\(\Rightarrow y=f\left(t\right)=4t^2-3t-1\)
Xét hàm \(f\left(t\right)\) trên \(\left[-1;1\right]\)
\(-\dfrac{b}{2a}=\dfrac{3}{8}\in\left[-1;1\right]\)
\(f\left(-1\right)=6\) ; \(f\left(\dfrac{3}{8}\right)=-\dfrac{25}{16}\) ; \(f\left(1\right)=0\)
\(\Rightarrow y_{min}=-\dfrac{25}{16}\) khi \(sinx=\dfrac{3}{8}\)
\(y_{max}=6\) khi \(sinx=-1\)
Chọn C
Nhận xét cosx = 0 không phải là nghiệm của phương trình. Do đó, nhân cả hai vế của phương trình cho cos ≠ 0ta được
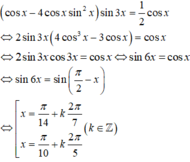
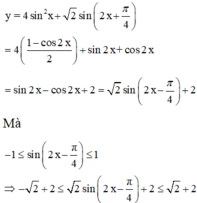
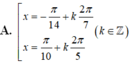
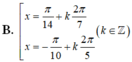
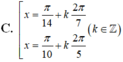
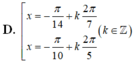
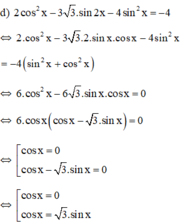
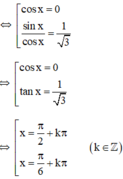
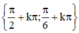(k ∈ Z)
Chọn C.
y' = cos2x – 2xsin2x;
y” = -2sin2x – (2sin2x + 4xcos2x) = -4sin2x – 4xcos2x.