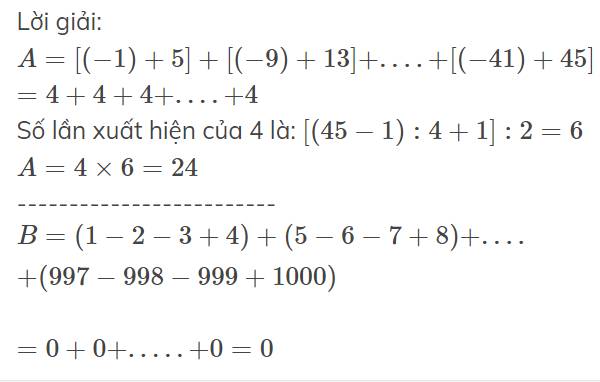K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
VN
0
AH
Akai Haruma
Giáo viên
9 tháng 12 2023
Lời giải:
$A=[(-1)+5]+[(-9)+13]+....+[(-41)+45]$
$=4+4+4+....+4$
Số lần xuất hiện của 4 là: $[(45-1):4+1]:2=6$
$A=4\times 6=24$
-------------------------
$B=(1-2-3+4)+(5-6-7+8)+....+(997-998-999+1000)$
$=0+0+.....+0=0$
NV
7
TH
12 tháng 7 2017
Cách 1 : Số số hạng là : ( 999 - 1 ) : 2 + 1 = 500 ( số )
Tổng là : ( 999 + 1 ) x 500 : 2 = 250000
Cách 2 : Có : ( 1 + 999 ) + ( 3 + 997 ) + ( 5 + 995 ) + ... + ( 499 + 501 )
= 1000 + 1000 + 1000 + ... + 1000
Nhìn dãy trên có tất cả 250 cặp
Vậy tổng là : 250 x 1000 = 250000
12 tháng 7 2017
Cách 1:
Từ 1 đến 1000 có 500 số chẵn và 500 số lẻ nên tổng trên có 500 số lẻ. Áp dụng các bài trên ta có C = (1 + 999) + (3 + 997) + ... + (499 + 501) = 1000.250 = 250.000 (Tổng trên có 250 cặp số)
đợi tí để mình làm cách 2
14 tháng 7 2016
a) 1 + 3 + 5 + 7 + 9 + ... + 997 + 999
=(999+1) + (3+997) + ...
=1000 x 250
=250000
b) 1 + 2 + 3 + 4 + ... + 1996
=(1996+1) + (2+1995) + ...
=1997 x 998
=1993006
c) 1 + 11 + 21 + 31 + ... + 981 + 991
=(1+991)+(11+981)+...
=992 x 50
=49600
10 tháng 8 2016
Số số hạng của dãy số trên là:
( 999 - 1 ): 1 + 1 = 889 ( số )
Tổng của dãy số trên là:
( 999 + 1 ) . 899 : 2 = 449500
k mik nha
SN
10 tháng 8 2016
Số số hạng dãy trên có là:
( 999 - 1 ) : 1 + 1 = 500 ( số hạng )
Tổng dãy trên là:
( 999 + 1 ) x 500 : 2 = 250000
Đáp số: 250000
NN
9
25 tháng 9 2017
\(1+3+5+...+997+999\)
\(=\frac{\left[\left(999-1\right):2+1\right].\left(999+1\right)}{2}\)
\(=250000\)