GK
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
1 tháng 11 2017
tổng số số hạng của dãy là: \(\left(\left(2n-1\right)^2-12\right):20+1\)chia 20 vì mỗi phần tử cách nhau 20 đơn vị
tổng của dãy : \(\frac{\left(\left(\left(2n-1\right)^2-12\right):20+1\right)\times\left(\left(2n-1\right)^2+12\right)}{2}\)
bài b tương tự ạ
CM
12 tháng 7 2017
Cách 1: Tính giá trị từng biểu thức trong ngoặc
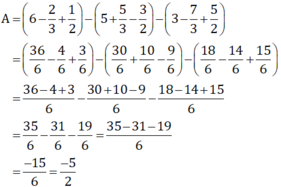
Cách 2: Bỏ dấu ngoặc rồi nhóm các số thích hợp
XN
1
29 tháng 3 2019
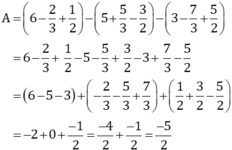
\(A=\frac{2^{12}\cdot27^3+20\cdot6^9}{2\cdot6^{10}+12^6\cdot3^5}\)
\(=\frac{2^{12}\cdot\left(3^3\right)^3+2^2\cdot5\cdot2^9\cdot3^9}{2\cdot2^{10}\cdot3^{10}+\left(2^2\right)^6\cdot3^6\cdot3^5}\)
\(=\frac{2^{12}\cdot3^9+2^{11}\cdot5\cdot3^9}{2^{11}\cdot3^{10}+2^{12}\cdot3^{11}}\)
\(=\frac{2^{11}\cdot3^9\left(2\cdot5\right)}{2^{11}\cdot3^{10}\left(2\cdot3\right)}\)
\(=\frac{2^{11}\cdot3^9\cdot10}{2^{11}\cdot3^{10}\cdot6}\)
\(=3\cdot\frac{10}{6}=\frac{30}{6}=5\)
PT
1
2 tháng 11 2021
Bài 1:
1) \(9A=3^3+3^5+...+3^{113}\)
\(\Rightarrow8A=9A-A=3^3+3^5+...+3^{113}-3-3^3-...-3^{111}=3^{113}-3\)
\(\Rightarrow A=\dfrac{3^{113}-3}{8}\)
2) \(9B=3^4+3^6+...+3^{202}\)
\(\Rightarrow8B=9B-B=3^4+3^6+...+3^{202}-3^2-3^4-...-3^{200}=3^{202}-3^2=3^{202}-9\)
\(\Rightarrow B=\dfrac{3^{202}-9}{8}\)
3) \(25C=5^3+5^5+...+5^{101}\)
\(\Rightarrow24C=25C-C=5^3+5^5+...+5^{101}-5-5^3-...-5^{99}=5^{101}-5\)
\(\Rightarrow C=\dfrac{5^{101}-5}{24}\)
4) \(25D=5^4+5^6+...+5^{102}\)
\(\Rightarrow24D=25D-D=5^4+5^6+...+5^{102}-5^2-5^4-...-5^{100}=5^{102}-25\)
\(\Rightarrow D=\dfrac{5^{102}-25}{24}\)
2 tháng 11 2021
Bài 2:
a) Gọi d là UCLN(2n+1,n+1)
\(\Rightarrow\left\{{}\begin{matrix}2n+1⋮d\\n+1⋮d\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}2n+1⋮d\\2n+2⋮d\end{matrix}\right.\)
\(\Rightarrow\left(2n+2\right)-\left(2n+1\right)⋮d\Rightarrow1⋮d\)
Vậy 2n+1 và n+1 là 2 số nguyên tố cùng nhau
\(\Rightarrow\dfrac{2n+1}{n+1}\) là phân số tối giản
b) Gọi d là UCLN(2n+3,3n+4)
\(\Rightarrow\left\{{}\begin{matrix}2n+3⋮d\\3n+4⋮d\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}6n+9⋮d\\6n+8⋮d\end{matrix}\right.\)
\(\Rightarrow\left(6n+9\right)-\left(6n+8\right)⋮d\Rightarrow1⋮d\)
\(\Rightarrow\dfrac{2n+3}{3n+4}\) là phân số tối giản
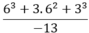
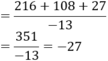
Ta có:
\(A=1+2.6+3.6^2+4.6^3+...+100.6^{99}\)
=> \(6A=6+2.6^2+3.6^3+....+99.6^{99}+100.6^{100}\)
=> A - 6A = \(1+6+6^2+6^3+...+6^{99}-100.6^{100}\)
=> \(-5A=1+6+6^2+...+6^{99}-100.6^{100}\)
Đặt: \(B=1+6+6^2+...+6^{99}\)
=> \(6B=6+6^2+6^3+...+6^{100}\)
=> 6 B - B = \(6^{100}-1\)
=> B = \(\frac{6^{100}-1}{5}\)
=> \(-5A=\frac{6^{100}-1}{5}-100.6^{100}\)
=> \(A=\frac{499.6^{100}+1}{25}\)