
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



2x+/x/=3x ( / / là giá trị tuyệt đối nha bạn )
/x/=3x-2x
/x/=x
Do giá trị tuyệt đối của bất kì số nguyên nào đều không bao giờ là số nguyên âm nên x phải lớn hơn -1
\(\Rightarrow x\in N\)
`2x+|x|=3x`
`=>|x|=3x-2x`
`=>|x|=x`
Sử dụng tính chất `|A|=|A|<=>A>=0`
`=>x>=0`
Vậy với `x>=0` thì `2x+|x|=3x`

e: =>-40+3+33+40-x=47
=>36-x=47
=>x=-11
f: =>x(x-3)(11-x)(11+x)=0
hay \(x\in\left\{0;3;11;-11\right\}\)
g: =>-62-38-x+2x=-100
=>x-100=-100
hay x=0

i: =>x-12-2x-31=6
=>-x-43=6
=>x+43=-6
hay x=-49
h: =>(x+1)=0
=>x=-1
f: =>x(x-3)(x+11)(x-11)=0
hay \(x\in\left\{0;3;-11;11\right\}\)

b: =>2/5*x=2/3+4/5=22/15
=>x=11/3
c: =>2,5-0,25(2-1/2x)=0,25
=>0,25(2-0,5x)=2,25
=>2-0,5x=9
=>-0,5x=-7
=>x=14
d: =>(x-3)^2=36
=>x=9 hoặc x=-3
e: =>1/2x-3/4=0 và x+y=25
=>x=15 và y=10

\(a,\Leftrightarrow x^3=\dfrac{20}{3}\Leftrightarrow x=\sqrt[3]{\dfrac{20}{3}}\\ b,\Leftrightarrow x-1=9\Leftrightarrow x=10\\ c,\Leftrightarrow\left[{}\begin{matrix}x-1=5\\x-1=-5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=6\\x=-4\end{matrix}\right.\\ d,\Leftrightarrow2x+1=5\Leftrightarrow x=2\\ e,\Leftrightarrow2x-4=4\Leftrightarrow x=4\)
Câu a) xem lại đề giùm nhé em
b) \(\left(x-1\right)^3=9^3\)
\(x-1=9\)
\(x=10\)
Vậy \(x=10\)
c) \(\left(x-1\right)^2=25\)
\(x-1=5\) hoặc \(x-1=-5\)
* \(x-1=5\)
\(x=6\)
* \(x-1=-5\)
\(x=-4\)
Vậy \(x=-4\); \(x=6\)
d) \(\left(2x+1\right)^3=125\)
\(\left(2x+1\right)^3=5^3\)
\(2x+1=5\)
\(2x=4\)
\(x=2\)
Vậy \(x=2\)
e) Sửa đề: \(\left(2x+4\right)^3=64\)
\(\left(2x+4\right)^3=4^3\)
\(2x+4=4\)
\(2x=0\)
\(x=0\)
Vậy \(x=0\)

a)
Để \(\left(3x-1\right).\left(-\frac{1}{2}x+5\right)=0\)=> 3x-1=0 hoặc \(-\frac{1}{2}x+5=0\)
=> x= \(\frac{1}{3}\) hoăc \(x=10\)
b)
\(\frac{1}{4}+\frac{1}{3}:\left(2x-1\right)=5\) => \(\frac{1}{3}:\left(2x-1\right)=5-\frac{1}{4}=\frac{19}{4}=>2x-1=\frac{1}{3}:\frac{19}{4}=\frac{4}{57}=>x=\frac{61}{114}\)
c) \(\left(2x+\frac{3}{5}\right)^2-\frac{9}{25}=0=>\left(2x+\frac{3}{5}\right)^2=\frac{9}{25}\)\(=>2x+\frac{3}{5}\in\left\{\pm\frac{3}{5}\right\}=>2x\in\left\{0;\frac{-6}{5}\right\}=>x\in\left\{0;\frac{-3}{5}\right\}\)
d) Xem lại đề
a) để (3x-1).(\(-\dfrac{1}{2}x+5\))=0
=> 3x-1 hoặc \(-\dfrac{1}{2}x+5\) =0
TH1 : 3x-1=0
3x = 0+1=1
x = 1:3 = \(\dfrac{1}{3}\)
TH2 : \(-\dfrac{1}{2}x+5\)= 0
\(-\dfrac{1}{2}x\)= 0 -5 = -5
x= -5 : \(-\dfrac{1}{2}\)
x= 10
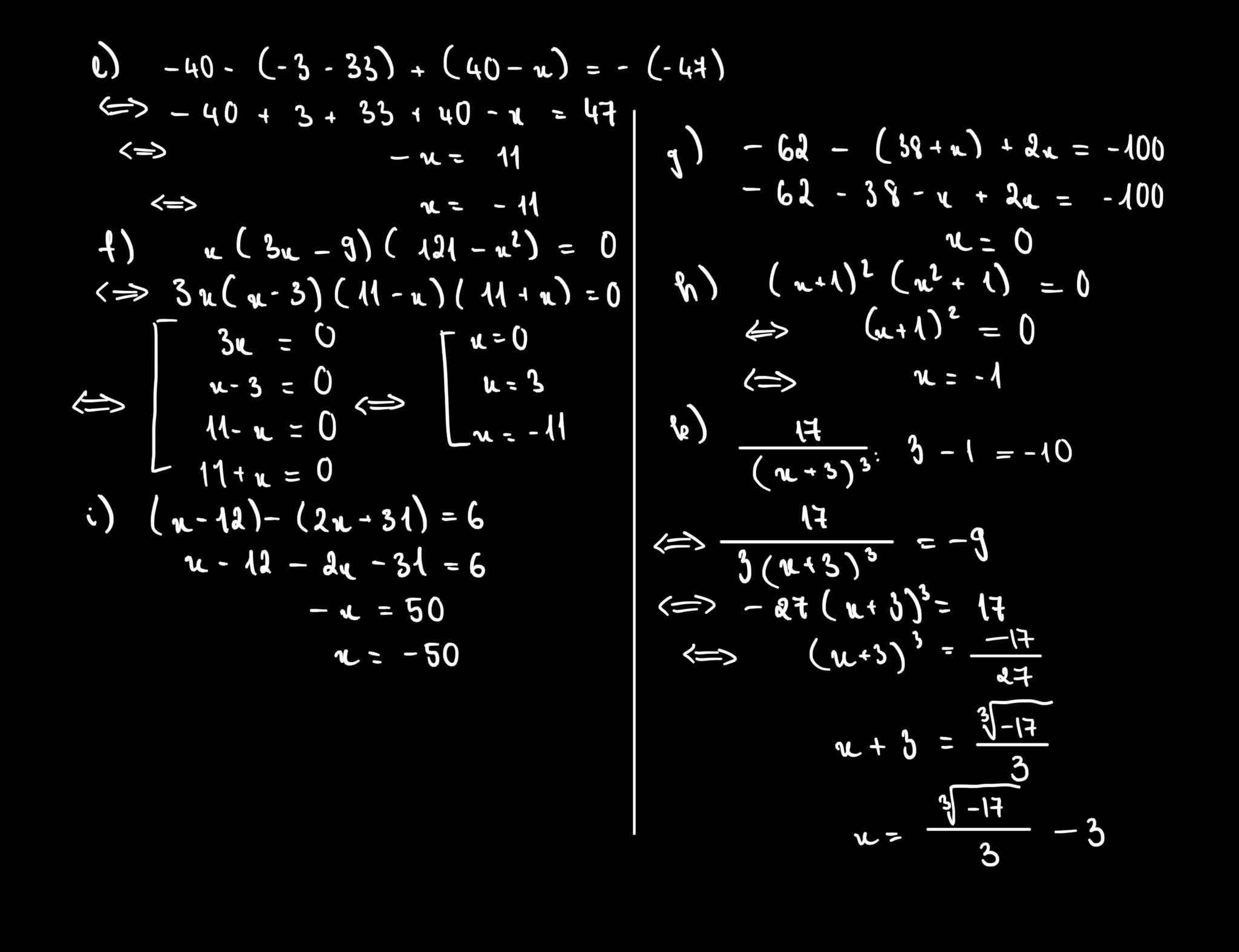
\(2^{x+1}+2^{x+3}=40\)
\(\Leftrightarrow2^x.2+2^x.2^3=40\)
\(\Leftrightarrow2^x.\left(2+8\right)=40\)
\(\Leftrightarrow2^x.10=40\)
\(\Leftrightarrow2^x=40:10\)
\(\Leftrightarrow2^x=4\)
\(\Leftrightarrow x=2\)
Vậy x=2