
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{4}=\dfrac{y}{-5}=\dfrac{-3x+2y}{-12-10}=\dfrac{55}{-22}=\dfrac{-5}{2}\)
Do đó: \(\left\{{}\begin{matrix}x=\dfrac{-20}{2}=-10\\y=\dfrac{25}{2}\end{matrix}\right.\)
b: Ta có: \(\dfrac{x}{y}=\dfrac{-7}{4}\)
nên \(\dfrac{x}{-7}=\dfrac{y}{4}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{-7}=\dfrac{y}{4}=\dfrac{4x-5y}{-28-20}=\dfrac{72}{-48}=\dfrac{-3}{2}\)
Do đó: \(\left\{{}\begin{matrix}x=\dfrac{21}{2}\\y=\dfrac{-12}{2}=-6\end{matrix}\right.\)

Ta có :
y và x là hai đại lượng tỉ lệ nghịch với nhau ⇒ y = a/x
Nên hệ số tỉ lệ a = x.y = 2.30 = 60

Bài 1: Ta có 200920 = (20092)10 = (2009.2009)10
2009200910 = (10001.2009)10
Mà 2009 < 10001 ➩ (2009.2009)10 < (10001.2009)10
Vậy 200920 < 2009200910

Nếu hai đại lượng y và x tỉ lệ nghịch với nhau theo hệ số tỉ lệ a thì:
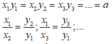
Đáp án cần chọn là C

Nếu hai đại lượng y và x tỉ lệ nghịch và y = 5 x nên hệ số tỉ lệ a = 5, do đó
x 1 y 1 = x 2 y 2 = x 3 y 3 = ... = 5
Đáp án cần chọn là C

Nếu hai đại lượng y và x tỉ lệ nghịch với nhau theo hệ số tỉ lệ a thì:
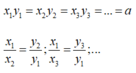
Chọn đáp án C
\(4x=3y\Rightarrow\frac{x}{3}=\frac{y}{4}\Rightarrow\frac{x^2}{9}=\frac{y^2}{16}\)
áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{x^2}{9}=\frac{y^2}{16}=\frac{x^2+y^2}{9+16}=\frac{400}{25}=16\)
suy ra:
\(\frac{x^2}{9}=16\Rightarrow x^2=144\Rightarrow x=12\)hoặc \(x=-12\)
\(\frac{y^2}{16}=16\Rightarrow y^2=256\Rightarrow y=16\)hoặc \(y=-16\)
Câu còn lại tương tự