Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, \(3x-8⋮x-4\)
\(3\left(x-4\right)+4⋮x-4\)
\(4⋮x-4\)hay \(x-4\inƯ\left(4\right)=\left\{\pm1;\pm2;\pm4\right\}\)
| x - 4 | 1 | -1 | 2 | -2 | 4 | -4 |
| x | 5 | 3 | 6 | 2 | 8 | 0 |
c, tương tự
a,Gợi ý:vì x^2+x+1 chia hết cho x+1 => x^2 chia hết cho x+1 b,Gợi ý nhân 3 với (x-4) rồi lấy 3x-8 trừ đi c,lấy (x+5) trừ đi x-2 e,Gợi ý x^2+2x-7 chia hết cho x+2

a)=>3(x2-1)+(5x+5)+3-5+8 chia hết cho x+1
=>3(x-1)(x+1)+5(x+1)+6 chia hết cho x+1
Mà 3(x-1)(x+1) và 5(x+1) chia hết cho x+1
=>6 chia hết cho x+1
=>x+1 thuộc Ư(6)={1;2;3;6;-1;-2;-3;-6}
=> x thuộc {0;1;2;5;-2;-3;-4;-7}
b) Ta có:(x2-4)+4-1 chia hết cho x+2
=>(x2-22)+3 chia hết cho x+2
=>(x-2)(x+2) +3 chia hết cho x+2
Mà (x-2)(x+2) chia hết cho x+2
=>3 chia hết cho x+2
=>x+2 thuộc Ư(3)={1;3;-1;-3}
=>x thuộc {-1;1;-3;-5}

a)<=>(x+1)+2 chia hết x+1
=>2 chia hết x+1
=>x+1\(\in\){1,-1,2,-2}
=>x\(\in\){0,-2,1,-3}
b)<=>3(x-2)+7 chia hết x-2
=>7 chia hết x-2
=>x-2\(\in\){1,-1,7,-7}
=>x\(\in\){3,1,9,-5}
c,d,e tương tự

a, x+3 chia hết cho x-1
Ta có: x+3=(x+1)+2
=> 2 chia hết cho x+1
=>x+1 thuộc Ư(2)= {1, -1, 2, -2}
=> x thuộc {0,-2, 1, -3}
b.
b,3x chia hết cho x-1
c,2-x chia hết cho x+1
Ta có:
\(\dfrac{x+3}{x-1}=\dfrac{x-1+4}{x-1}=1+\dfrac{4}{x-1}\)
Để (x + 3) \(⋮\left(x-1\right)\) thì 4 \(⋮\left(x-1\right)\)
\(\Rightarrow\) x - 1 = 1; x - 1 = -1; x - 1 = 2; x - 1 = -2; x - 1 = 4; x - 1 = -4
*) x - 1 = 1
x = 2
*) x - 1 = -1
x = 0
*) x - 1 = 2
x = 3
*) x - 1 = -2
x = -1
*) x - 1 = 4
x = 5
*) x - 1 = -4
x = -3
Vậy x = 5; x = 3; x = 2; x = 0; x = -1; x = -3
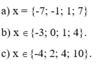
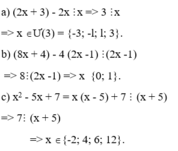
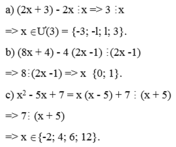
a, x^2+x+1= x(x+1)+1
Vì x(x+1) chia hết cho x+1 nên x(x+1)+1 chia hết cho x+1 khi và chỉ khi 1 chia hết cho x+1
⇒ x+1=-1 hoặc x+1=1
⇒ x=-2 hoặc x=0
b, 3x-8=3x-12+4=3(x-4)+4
Vì 3(x-4) chia hết cho x-4 nên 3(x-4)+4 chia hết cho x-4 khi và chỉ khi 4 chia hết cho x-4
⇒ x-4 ∈{-4,-2,-1,1,2,4}
⇒ x ∈{0,2,3,5,6,8}
đúng thì link nhé chúc học tốt!!!!!!
\(x^2+x+1\)\(⋮\text{ }x+1\)
\(\Rightarrow x\left(x+1\right)+1\)\(⋮\text{ }x+1\)
\(\Rightarrow1\text{}\)\(⋮\text{ }x+1\)\(\Rightarrow x+1\)\(\inƯ\left(1\right)=\left\{\pm1\right\}\)