
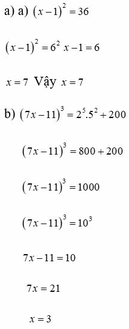
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

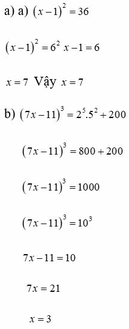

a;\(\dfrac{-6}{11}\) : \(\dfrac{12}{55}\) = \(\dfrac{-5}{2}\)
b;\(\dfrac{7}{12}\) + \(\dfrac{5}{72}\) - \(\dfrac{11}{36}\) = \(\dfrac{47}{72}\) - \(\dfrac{11}{36}\) = \(\dfrac{25}{72}\)
c;\(\dfrac{13}{10}\) : \(\dfrac{-5}{13}\) = \(\dfrac{-169}{50}\)
d; {\(\dfrac{5}{12}\) + \(\dfrac{5}{11}\) } : { \(\dfrac{5}{3}\) -\(\dfrac{7}{11}\) } = \(\dfrac{115}{132}\) : \(\dfrac{34}{33}\) = \(\dfrac{115}{136}\)
lưu ý mk ko chép đầu bài
mình cần gấp lắm đến chiều mai là phải nộp rùi
giúp mình nha thanks cá bạn trước ![]() ko có tâm trạng mà cười nữa
ko có tâm trạng mà cười nữa![]()
![]()

a) \(2^x+5=21\)
\(\Rightarrow2^x=21-5=16\Rightarrow2^x=2^4\)
Vậy x = 4
b) \(2^x-1+3^2=5^2+2.5\)
\(\Rightarrow2^x-1+9=35\)
\(\Rightarrow2^x=35-9+1=27\)
Vậy x không có giá trị
c;d;e;f làm tương tự

B=\(6\frac{4}{9}-4\frac{4}{9}+3\frac{7}{11}\)
B=\(2+3\frac{7}{11}\)
B=\(5\frac{7}{11}\)
B = \(5\frac{7}{11}=\frac{62}{11}\)
C = 1
D = \(\frac{5}{2}=2\frac{1}{2}\)

a) \(|x+1|=3\)
\(\Rightarrow x+1=\pm3\)
+) \(x+1=3\) +) \(x+1=-3\)
\(\Rightarrow x=2\) \(\Rightarrow x=-4\)
Vậy \(x\in\left\{2;-4\right\}\)
b) \(3^2x+2^4=5^2\)
\(9x+16=25\)
\(9x=25-16\)
\(9x=9\)
\(x=1\)
c) \(\frac{4+x}{7+y}=\frac{4}{7}\)
\(\Rightarrow\left(4+x\right).7=\left(7+y\right).4\)
\(\Rightarrow28+7x=28+4y\)
\(\Rightarrow7x=4y\)
Mà \(\left(7,4\right)=1\) và \(x+y=11\)
Vậy \(x=4;y=7\)
a) Ta có: \(\left|x+1\right|=3\)
\(\Rightarrow x+1=\pm3\)
Nếu x + 1 = 3 => x = 2
Nếu x + 1 = -3 => x = -4
Vậy x = {2;-4}
b) \(3^2x+2^4=5^2\)
\(\Rightarrow9x+16=25\)
\(\Rightarrow9x=9\)
\(\Rightarrow x=1\)
Vậy x = 1
c) \(\frac{4+x}{7+x}=\frac{4}{7}\)
\(\Rightarrow7\left(4+x\right)=4\left(7+x\right)\)
\(\Rightarrow28+7x=28+4x\)
\(\Rightarrow7x-4x=0\)
\(\Rightarrow x=0\)
Vậy x = 0

Bạn ơi ; tách từng bài ra cho dễ làm :
1.7C-C= 7^2016-7
C = ( 7^2016-7 ) :6
\(C=7+7^2+7^3+.....+7^{2016}\)
\(\Rightarrow7C=7^2+7^3+7^4+...+7^{2017}\)
\(\Rightarrow7C-C=\left(7^2+7^3+.....+7^{2017}\right)-\left(7+7^2+7^3+....+7^{2016}\right)\)
\(\Rightarrow6C=2^{2017}-7\)
\(\Rightarrow C=\frac{2^{2017}-7}{6}\)