
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


x^2 + 2x - 5 ⋮ x + 1 <=> ( x^2 + 2x + 1 ) - 6 ⋮ x + 1
=> ( x + 1 )2 - 6 ⋮ x + 1
Vì ( x + 1 )2 ⋮ x + 1 ∀ x ∈ Z
Để ( x + 1 )2 - 6 ⋮ x + 1 <=> 6 ⋮ x + 1 => x + 1 ∈ Ư ( 6 )
=> Ư ( 6 ) = { - 6 ; - 3 ; - 2 ; - 1 ; 1 ; 2 ; 3 ; 6 }
=> x ∈ { - 7 ; - 4 ; - 3 ; - 2 ; 0 ; 1 ; 2 ; 5 }


x + 9 ⋮ x + 1
\(\Rightarrow\) x + 1 + 8 ⋮ x+1
\(\Rightarrow\) 8 ⋮ x + 1
\(\Rightarrow x+1\inƯ\left(8\right)=\left\{1;-1;2;-2;4;-4;8;-8\right\}\)
Mà: \(x\in N\)
\(\Rightarrow x+1\in\left\{1;2;4;8\right\}\)
| x+1 | 1 | 2 | 4 | 8 |
| x | 0 | 1 | 3 | 7 |
\(\Rightarrow x\in\left\{0;1;3;7\right\}\)
a: x+9 chia hết cho x+1
=>x+1+8 chia hết cho x+1
=>8 chia hết cho x+1
=>x+1 thuộc {1;2;4;8}
=>x thuộc {0;1;3;7}
b: 2x+1 chia hết cho x-1
=>2x-2+3 chia hết cho x-1
=>3 chia hết cho x-1
=>x-1 thuộc {-1;1;3}
=>x thuộc {0;2;4}
Tìm x thuộc N :
a) 2x + 1 chia hết cho x + 2
b) 5x + 2 chia hết cho x + 1
c) 3x + 1 chia hết cho 2x + 1

a) Ta có: \(2x+1=\left(2x+4\right)-3=2.\left(x+2\right)-3\)
- Để \(2x+1⋮x+2\)\(\Leftrightarrow\)\(2.\left(x+2\right)-3⋮x+2\)mà \(2.\left(x+2\right)⋮x+2\)
\(\Rightarrow\)\(3⋮x+2\)\(\Rightarrow\)\(x+2\inƯ\left(3\right)\in\left\{\pm1;\pm3\right\}\)
- Ta có bảng giá trị:
| \(x+2\) | \(-1\) | \(1\) | \(-3\) | \(3\) |
| \(x\) | \(-3\) | \(-1\) | \(-5\) | \(1\) |
| \(\left(TM\right)\) | \(\left(TM\right)\) | \(\left(TM\right)\) | \(\left(TM\right)\) |
Vậy \(x\in\left\{-5,-3,-1,1\right\}\)
b) Ta có: \(5x+2=\left(5x+5\right)-3=5.\left(x+1\right)-3\)
- Để \(5x+2⋮x+1\)\(\Leftrightarrow\)\(5.\left(x+1\right)-3⋮x+1\)mà \(5.\left(x+1\right)⋮x+1\)
\(\Rightarrow\)\(3⋮x+1\)\(\Rightarrow\)\(x+1\inƯ\left(3\right)\in\left\{\pm1;\pm3\right\}\)
- Ta có bảng giá trị:
| \(x+1\) | \(-1\) | \(1\) | \(-3\) | \(3\) |
| \(x\) | \(-2\) | \(0\) | \(-4\) | \(2\) |
| \(\left(TM\right)\) | \(\left(TM\right)\) | \(\left(TM\right)\) | \(\left(TM\right)\) |
Vậy \(x\in\left\{-4,-2,0,2\right\}\)
c) Để \(3x+1⋮2x+1\)\(\Leftrightarrow\)\(2.\left(3x+1\right)⋮2x+1\)
- Ta có: \(2.\left(3x+1\right)=6x+2=\left(6x+3\right)-1=3.\left(2x+1\right)-1\)
- Để \(2.\left(3x+1\right)⋮2x+1\)\(\Leftrightarrow\)\(3.\left(2x+1\right)-1⋮2x+1\)mà \(3.\left(2x+1\right)⋮2x+1\)
\(\Rightarrow\)\(1⋮2x+1\)\(\Rightarrow\)\(2x+1\inƯ\left(1\right)\in\left\{\pm1\right\}\)
+ \(2x+1=1\)\(\Leftrightarrow\)\(2x=0\)\(\Leftrightarrow\)\(x=0\left(TM\right)\)
+ \(2x+1=-1\)\(\Leftrightarrow\)\(2x=-2\)\(\Leftrightarrow\)\(x=-1\left(TM\right)\)
Vậy \(x\in\left\{-1,0\right\}\)
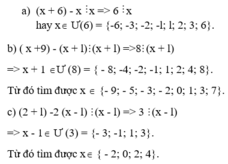
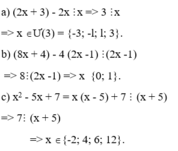
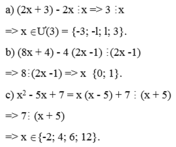
x2 + 2x chia hết cho x + 1
Mà x.(x + 1) chia hết cho x + 1
hay x2 + x chia hết cho x + 1
=> [(x2 + 2x) - (x2 + x)] chia hết cho x + 1
=> x chia hết cho x + 1
=> x + 1 - 1 chia hết cho x + 1
Mà x + 1 chia hết cho x + 1
=> 1 chia hết cho x + 1
=> x + 1 thuộc Ư (1) = {-1; 1}
=> x thuộc {-2; 0}.