NM
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
5 tháng 3 2015
Nếu ở cuối là = 2013.1007 thì phương trình có nghiệm là x = 1 Vì:
Ta thực hiện thao tác nhóm như sau:
(x+2012x) + (2x+2011x) + (3x+2010x) + ....+ 2013x = 2013.1007
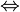2013x + 2013x + 2013x + ...+ 2013x = 2013.1007
có tất cả 1006 số 2013x cộng với 2013x = 2013.1007
Vậy: 1006.2013x + 2013x = 2013.1007
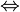(1006 + 1)2013x = 2013.1007 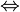x = (2013.1007)/[(1006+1)2013] = 1
13 tháng 3 2016
X=1
Ko sai
Bai nay lam roi
Ap dung ct tinh tong so hang cua 1 day so
roi the vao
HP
10 tháng 3 2016
x+2x+3x+.....+2013x=2013.2017
=>x.(1+2+3+.....+2013)=2013.2017
=>\(x.\frac{2013.\left(2013+1\right)}{2}=2013.2017\Rightarrow x.2027091=4060221\Rightarrow x=\frac{2017}{1007}\)
4 tháng 3 2016
x.(1+2+3+....+2013)=2013.2017
x.2027091 = 20271091
x = 202710901/2027091
x=1
sai thi thui ><
5 tháng 7 2016
Đặt \(g\left(x\right)=x^{2015}-x^{2014}+x^{2013}-...+x-1\)
Dễ thấy: \(f\left(x\right)=x^{2016}-2013\times g\left(x\right)\Rightarrow f\left(2012\right)=2012^{2016}-2013\times g\left(2012\right)\)(a)
Ta có: \(\left(x+1\right)\times g\left(x\right)=\left(x+1\right)\left(x^{2015}-x^{2014}+x^{2013}-...+x-1\right)\)
\(\Rightarrow\left(x+1\right)\times g\left(x\right)=x^{2016}-1\)
\(\Rightarrow\left(2012+1\right)\times g\left(2012\right)=2012^{2016}-1\)hay: \(2013\times g\left(2012\right)=2012^{2016}-1\)
Thay vào (a) ta có: \(f\left(2012\right)=2012^{2016}-\left(2012^{2016}-1\right)=1\).
NH
30 tháng 5 2020
f(x) = x2013 - 2013x2012 + 2013x2011 - 2013x2010 + .... + 2013x - 1
= x2013 - (2012 + 1)x2012 + (2012 + 1)x2011 - (2012 + 1)x2010 + .... + (2012 + 1)x - 1
= x2013 - (x + 1)x2012 + (x + 1)x2011 - (x + 1)x2010 + .... + (x + 1)x - 1
= x2013 - x . x2012 - 1 . x2012 + x . x2011 + 1 . x2011 - x . x2010 - 1 . x2010 + ... + x . x + 1 . x - 1
= x2013 - x2013 - x2012 + x2012 + x2011 - x2011 - x2010 + .... + x2 + x - 1
= x - 1 = 2012 - 1 = 2011
=>x.(1+2+3+..+2013)=2013
=>x. [2013.(2013+1)]/2=2013
=>x.2027091=2013
=>x=2013/2027091=1/1007