Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1. Gấp hình 33.a theo các nét đã chỉ ra thì có được một hình hộp chữ nhật.
2. a) Trong hình hộp ABCD.EFGH thì:
+) BF vuông góc với hai đường thẳng cắt nhau EF và FG của mặt phẳng (EFGH) nên BF vuông góc với mặt phẳng (EFGH).
+) BF vuông góc với hai đường thẳng cắt nhau AB và BC của mặt phẳng (ABCD) nên BF vuông góc với mặt phẳng (ABCD).
b) Hai mặt phẳng (AEHD) và (CGHD)vuông góc với nhau vì mặt phẳng (AEHD) chứa đường thẳng EH vuông góc với mặt phẳng (CGHD).

1. Gấp hình 33a theo các nét đã chỉ ra thì có được một hình hộp chữ nhật
2. a) Trong hình hộp ABCD.EFGH thì:
BF song song với mp (DHGC) và mp (DHEA).
b) Hai mặt phẳng (AEHD) và (CGHD) vuông góc với nhau vì mặt phẳng (AEHD) chứa đường thẳng EH vuông

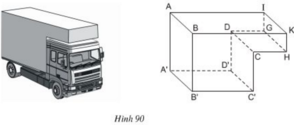
a) Những đường thẳng song song với mặt phẳng (ABKI) là A’B’; D’C’; DC; GH.
b) Những đường thẳng vuông góc với mặt phẳng (DCC'D') là A'D'; B'C'; DG; CH; AI; BK.
c) Ta có: A'D' ⊥ (CDD'C') mà A’D’ nằm trong mặt phẳng (A’D’C’B’) nên (A'B'C'D') ⊥ (CDD'C')

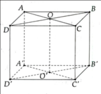
a) Không vì AA' ≠ AB.
b) HS tự chứng minh.
c) Giao tuyến là OO'.
d) Chiều cao là 5 7 c m

Tương tự 1A
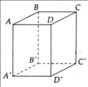
a) AB' và C'D song song, B'D' và AD chéo nhau, AC và A'C' song song.
b) BC' song song với (ADD'A').
c) AC' và CA' cắt nhau tại C.
d) (ACC'A') và (BDD'B') cắt nhau theo giao tuyến OO' (O và O' lần lượt là giao của AC, BD và A'C', B'D')

Lời giải
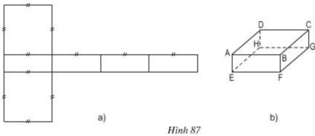
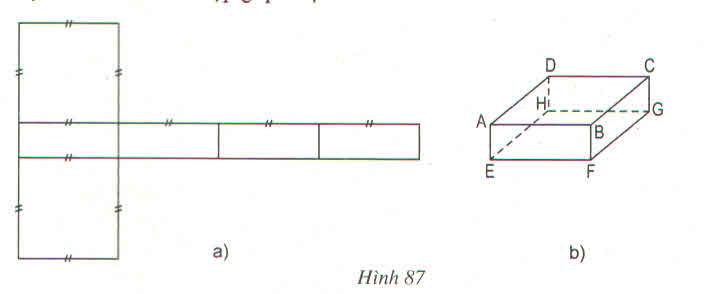
1. Gấp hình 87a theo các nét đã chỉ ra thì có được một hình hộp chữ nhật.
2. a) Trong hình hộp ABCD.EFGH thì:
BF song song với mp (DHGC) và (DHEA)
b) Hai mặt phẳng (AEHD) và (CGHD)vuông góc với nhau vì mặt phẳng (AEHD) chứa đường thẳng EH vuông góc với mặt phẳng (CGHD) chứa đường thẳng EH vuông góc với mặt phẳng (CGHD) tại H.
1. Gấp hình 87a theo các nét đã chỉ ra thì có được một hình hộp chữ nhật.
2. a) Trong hình hộp ABCD.EFGH thì:
BF song song với mp (DHGC) và (DHEA)
b) Hai mặt phẳng (AEHD) và (CGHD)vuông góc với nhau vì mặt phẳng (AEHD) chứa đường thẳng EH vuông góc với mặt phẳng (CGHD) chứa đường thẳng EH vuông góc với mặt phẳng (CGHD) tại H.
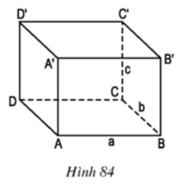



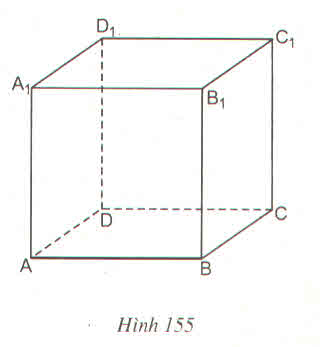

- Các đường thẳng vuông góc với mặt phẳng (ABCD) : AA', BB', CC', DD'
- Đường thẳng AB có nằm trong mặt phẳng (ABCD) vì hai điểm A, B thuộc mặt phẳng (ABCD)
- Đường thẳng AB vuông góc với hai đường thẳng cắt nhau AD và AA’ của mặt phẳng (ADD'A') nên AB vuông góc với mặt phẳng (ADD'A').