Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(\overrightarrow{a}\left(2;3\right)\);
b) \(\overrightarrow{b}\left(\dfrac{1}{3};-5\right)\);
c) \(\overrightarrow{c}\left(3;0\right)\);
d) \(\overrightarrow{d}\left(0;-2\right)\).

a) Vì \(\overrightarrow a = 3\overrightarrow i \)nên \(\overrightarrow a = \left( {3;0} \right)\)
b) Vì \(\overrightarrow b = - \overrightarrow j \)nên \(\overrightarrow b = \left( {0; - 1} \right)\)
c) Vì \(\overrightarrow c = \overrightarrow i - 4\overrightarrow j \)nên \(\overrightarrow c = \left( {1; - 4} \right)\)
d) Vì \(\overrightarrow d = 0,5\overrightarrow i + \sqrt 6 \overrightarrow j \)nên \(\overrightarrow d = \left( {0,5;\sqrt 6 } \right)\)

Lời giải:
$\overrightarrow{i}=(1,0), \overrightarrow{j}=(0,1)$
$\Rightarrow \overrightarrow{i}-\overrightarrow{j}=(1-0,0-1)=(1,-1)$
Bài 2:
$\overrightarrow{a}+2\overrightarrow{b}=(3+2.-1, -4+2.2)=(1, 0)$

Tham khảo:
a) Ta có: \(\overrightarrow b = \left( {4; - 1} \right)\) và \(\overrightarrow a = 3.\overrightarrow i - 2.\overrightarrow j \;\; \Rightarrow \;\overrightarrow a \;\left( {3; - 2} \right)\)
\( \Rightarrow 2\;\overrightarrow a - \overrightarrow b = \left( {2.3 - 4\;;\;2.\left( { - 2} \right) - \left( { - 1} \right)} \right) = \left( {2; - 3} \right)\)
Lại có: M (-3; 6), N(3; -3)
\( \Rightarrow \overrightarrow {MN} = \left( {3 - \left( { - 3} \right); - 3 - 6} \right) = \left( {6; - 9} \right)\)
Dễ thấy:\(\left( {6; - 9} \right) = 3.\left( {2; - 3} \right)\) \( \Rightarrow \overrightarrow {MN} = 3\left( {2\;\overrightarrow a - \overrightarrow b } \right)\)
b) Ta có: \(\overrightarrow {OM} = \left( { - 3;6} \right)\) ( do M(-3; 6)) và \(\overrightarrow {ON} = \left( {3; - 3} \right)\) (do N (3; -3)).
Hai vectơ này không cùng phương (vì \(\frac{{ - 3}}{3} \ne \frac{6}{{ - 3}}\)).
Do đó các điểm O, M, N không cùng nằm trên một đường thẳng.
Vậy chúng không thẳng hàng.
c) Các điểm O, M, N không thẳng hàng nên OMNP là một hình hành khi và chỉ khi \(\overrightarrow {OM} = \overrightarrow {PN} \).
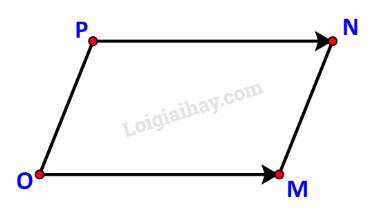
Do \(\overrightarrow {OM} = \left( { - 3;6} \right),\;\overrightarrow {PN} = \left( {3 - x; - 3 - y} \right)\) nên
\(\overrightarrow {OM} = \overrightarrow {PN} \Leftrightarrow \left\{ \begin{array}{l} - 3 = 3 - x\\6 = - 3 - y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 6\\y = - 9\end{array} \right.\)
Vậy điểm cần tìm là P (6; -9).

TenAnh1
TenAnh1
A = (-4.34, -5.84)
A = (-4.34, -5.84)
A = (-4.34, -5.84)
B = (11.02, -5.84)
B = (11.02, -5.84)
B = (11.02, -5.84)
Hình thoi nhận O là tâm đối xứng.
\(\left|x_A\right|=\left|x_C\right|=2AC\)\(\Rightarrow\left|x_A\right|=\left|x_C\right|=8:2=4\).
Do \(\overrightarrow{OC}\) và \(\overrightarrow{i}\) cùng hướng nên \(x_C=4;x_A=-4\).
A, C nằm trên trục hoành nên \(y_A=y_C=0\).
Vậy \(A\left(-4;0\right);C\left(4;0\right)\).
\(\left|y_B\right|=\left|y_D\right|=2BD\)\(\Rightarrow\left|y_B\right|=\left|y_D\right|=6:2=3\).
Do \(\overrightarrow{OB}\) và \(\overrightarrow{j}\) cùng hướng nên \(y_B=3;y_D=-3\).
B, D nằm trên trục tung nên \(x_B=x_D=0\).
Vậy \(B\left(0;3\right);D\left(0;-3\right)\).
b) \(x_I=\dfrac{x_B+x_C}{2}=\dfrac{0+4}{2}=2\); \(y_I=\dfrac{y_B+y_C}{2}=\dfrac{3+0}{2}=\dfrac{3}{2}\).
Vậy \(I\left(2;\dfrac{3}{2}\right)\).
\(x_G=\dfrac{x_A+x_B+x_C}{3}=\dfrac{-4+0+4}{3}=0\).
\(y_G=\dfrac{y_A+y_B+y_C}{3}=\dfrac{0+3+0}{3}=1\).
Vậy \(G\left(0;1\right)\).
c) I' đối xứng với I qua tâm O nên \(I'\left(-2;-\dfrac{3}{2}\right)\).
d) \(\overrightarrow{AC}\left(8;0\right);\overrightarrow{BD}\left(0;-6\right);\overrightarrow{BC}\left(4;-3\right)\).

a) Ta có hai vectơ \(\overrightarrow i \) và \(\overrightarrow j \) vuông góc nên \(\overrightarrow i .\overrightarrow j = 0\)
+) \({\left( {\overrightarrow i + \overrightarrow j } \right)^2} = {\left( {\overrightarrow i } \right)^2} + {\left( {\overrightarrow j } \right)^2} + 2\overrightarrow i .\overrightarrow j = {\left| {\overrightarrow i } \right|^2} + {\left| {\overrightarrow j } \right|^2} = 1 + 1 = 2\)
+) \({\left( {\overrightarrow i + \overrightarrow j } \right)^2} = {\left( {\overrightarrow i } \right)^2} + {\left( {\overrightarrow j } \right)^2} - 2\overrightarrow i .\overrightarrow j = {\left| {\overrightarrow i } \right|^2} + {\left| {\overrightarrow j } \right|^2} = 1 + 1 = 2\)
+) \(\left( {\overrightarrow i + \overrightarrow j } \right)\left( {\overrightarrow i - \overrightarrow j } \right) = {\left( {\overrightarrow i } \right)^2} - {\left( {\overrightarrow j } \right)^2} = {\left| {\overrightarrow i } \right|^2} - {\left| {\overrightarrow j } \right|^2} = 1 - 1 = 0\)
b) Sử dụng kết quả của câu a) ta có:
\(\overrightarrow a .\overrightarrow b = \left( {2\overrightarrow i + 2\overrightarrow j } \right).\left( {3\overrightarrow i - 3\overrightarrow j } \right) = 2.3.\left( {\overrightarrow i + \overrightarrow j } \right).\left( {\overrightarrow i - \overrightarrow j } \right) = 6.0 = 0\)
\(\overrightarrow a .\overrightarrow b = 0 \Rightarrow \overrightarrow a \bot \overrightarrow b \Rightarrow \left( {\overrightarrow a ,\overrightarrow b } \right) = 90^\circ \)
a) Tọa độ của vectơ \(\overrightarrow a \) là \(\left( {2;7} \right)\)
b) Tọa độ của vectơ \(\overrightarrow b \) là \(\left( { - 1;3} \right)\)
c) Tọa độ của vectơ \(\overrightarrow c \) là \(\left( {4;0} \right)\)
d) Tọa độ của vectơ \(\overrightarrow d \) là \(\left( {0; - 9} \right)\)