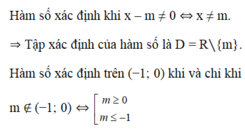Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ĐKXĐ: \(\left\{{}\begin{matrix}x-m+1\ge0\\-x+2m>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge m-1\\x< 2m\end{matrix}\right.\)
\(\Rightarrow x\in[m-1;2m)\)
Để hàm xác định trên (3;4)
\(\Rightarrow\left(3;4\right)\subset[m-1;2m)\)
\(\Rightarrow\left\{{}\begin{matrix}m-1\le3\\2m\ge4\end{matrix}\right.\) \(\Rightarrow2\le m\le4\)

\(\left\{{}\begin{matrix}m\le x\\x\le3\end{matrix}\right.\Rightarrow m\le3\Rightarrow\left[m;3\right]\)
Vay \(m\le3\) thi ham so co tap xd la 1 doan tren truc so
P/s: Ve cai truc so ra la hieu

Để hàm số xác định thì x-m+2>=0 và x-m+2<>1
=>x>=m-2 và x<>m-1
=>m-2<=0 và \(m-1\notin\left(0;1\right)\)
=>m<=2 và (m-1<=0 hoặc m-1>=1)
=>m=2 hoặc m<=1

Để y xác định thì \(\left(m-2\right)x+2m-3\ge0\forall x\in\left[-1;4\right]\)
\(\Leftrightarrow mx-2x+2m-3\ge0\)
\(\Leftrightarrow m\left(x+2\right)-2x-3\ge0\)
\(\Leftrightarrow m\ge\dfrac{2x+3}{x+2}\left(x+2>0\forall x\in\left[-1;4\right]\right)\)
\(\Rightarrow1\le m\le\dfrac{11}{6}\)

Hàm xác định trên \(\left[2;3\right]\) khi và chỉ khi:
\(x^2-2x-m>0;\forall x\in\left[2;3\right]\)
\(\Rightarrow x^2-2x>m;\forall x\in\left[2;3\right]\)
\(\Rightarrow m< \min\limits_{\left[2;3\right]}\left(x^2-2x\right)\)
Xét hàm \(f\left(x\right)=x^2-2x\) trên \(\left[2;3\right]\)
\(-\dfrac{b}{2a}=1\notin\left[2;3\right]\)
\(f\left(2\right)=0\) ; \(f\left(3\right)=3\)
\(\Rightarrow\min\limits_{\left[2;3\right]}\left(x^2-2x\right)=0\)
\(\Rightarrow m< 0\)