Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B
Để hàm số đã cho có tập xác định là R khi và chỉ khi : x2- 2x-m+ 1> 0 với mọi x
Hay
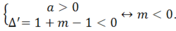

Chọn D
Hàm số y = log ( x 2 - 4 x - m + 1 ) có tập xác định là ℝ khi và chỉ khi
![]()
![]()

Chọn D
y = log ( x 2 - 2 m x + 4 )
Điều kiện xác định của hàm số trên ![]()
Để tập xác định của hàm số là
ℝ
thì 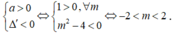
Vậy đáp án đúng là đáp án D.

Chọn A.
Đặt t = log3x .
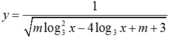 trở thành
trở thành 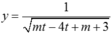
Hàm số 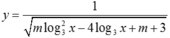 xác định trên khoảng (0: +∞ ) khi và chỉ khi
xác định trên khoảng (0: +∞ ) khi và chỉ khi ![]() xác định trên R.
xác định trên R.
Do đó; mt2 - 4t + m + 3 > 0 mọi x
Nên ∆’ = 4- m2 -3m < 0
Suy ra m < -4 hoặc m > 1.
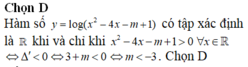




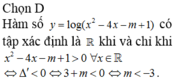
Chọn A
Cách 1
Điều kiện: x > 0
Hàm số xác định khi:
Để hàm số xác định trên ( 0 ; + ∞ ) thì phương trình
Xét hàm số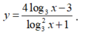
Đặt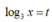 khi đó ta có
khi đó ta có
Ta có BBT:
Để hàm số xác định trên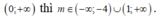
Cách 2:
Đề hàm số xác định trên khoảng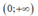 thi phương trình
thi phương trình  vô nghiệm.
vô nghiệm.
TH1: m = 0 thì PT trở thành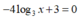
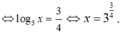
Vậy m = 0 không thỏa mãn.
TH2: m ≠ 0 thì để PT vô nghiệm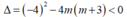
Để hàm số xác định trên